题目内容
如图,在梯形△ABCD中,AB//CD,AD=DC-=CB=1,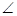 ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.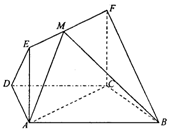
(1)求证:BC⊥平面ACFE;
(2)若M为线段EF的中点,设平面MAB与平面FCB所成角为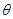 ,求
,求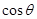 .
.
(1)在梯形 中
中


 平面
平面 平面
平面

 平面
平面 (2)
(2)
解析试题分析:(1)证明:在梯形 中,
中, ,
, ,
, ,
, 平面
平面 平面
平面 ,平面
,平面 平面
平面 平面
平面 ,
,
 平面
平面 。
。
(2)由(1)可建立分别以直线 为
为 轴,
轴, 轴,
轴, 轴的空间直角坐标系,则
轴的空间直角坐标系,则
 ,
,
设 是平面
是平面 的一个法向量,
的一个法向量,
由 ,得
,得 ,取
,取 ,得
,得 ,
,
 是平面
是平面 的一个法向量,
的一个法向量,
考点:空间线面垂直的判定及二面角大小
点评:利用空间向量的方法求解立体几何问题时思路简单,主要步骤:建立空间坐标系,找到相关点的坐标及向量,代入相应的公式计算即可

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 是正三角形,AB
是正三角形,AB 平面BCD,
平面BCD, ,E为BC的中点,F在棱AC上,且
,E为BC的中点,F在棱AC上,且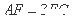

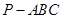 中,
中,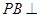 底面
底面 于
于 ,
, ,
, ,点
,点 是
是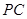 的中点.
的中点.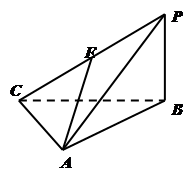
 平面
平面 ;
; 与
与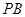 所成的角为
所成的角为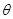 ,且
,且 ,
,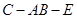 的大小.
的大小.  中,侧棱与底面垂直,
中,侧棱与底面垂直, ,
,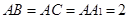 ,点
,点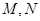 分别为
分别为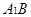 和
和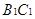 的中点.
的中点.
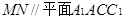 ;
; 的正弦值.
的正弦值. 棱长为1,
棱长为1, 是
是 的中点,
的中点, 是
是 的中点.
的中点. 
 ;
; 的余弦值.
的余弦值. ; (2)求证:
; (2)求证: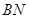
 ;
; 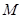 为
为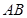 中点,在
中点,在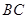 边上找一点
边上找一点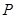 ,使
,使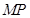
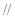 平面
平面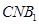 ,并求
,并求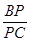 的值.
的值.
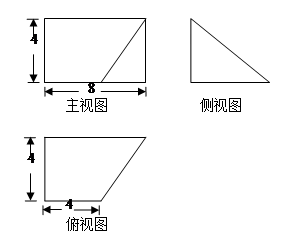

 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形,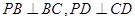 ,且
,且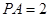 ,
,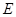 为
为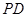 中点.
中点.
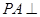 平面
平面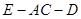 的大小;
的大小; 上是否存在点
上是否存在点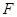 ,使得点
,使得点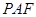 的距离为
的距离为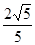 ?若存在,确定点
?若存在,确定点