题目内容
如图,正方体 棱长为1,
棱长为1, 是
是 的中点,
的中点, 是
是 的中点.
的中点. 
(1)求证: ;
;
(2)求二面角 的余弦值.
的余弦值.
(1)建立空间直角坐标系来表示平面的法向量于直线的方向向量,来根据垂直关系来得到证明。(2) 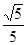
解析试题分析:(1)证明:以D为坐标原点,直线DA,DC,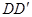 分别为x, y, z轴,
分别为x, y, z轴,
建立空间直角坐标系, 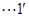
则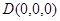 ,A(1,0,0),
,A(1,0,0), 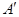 (1,0,1),
(1,0,1),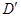 (0,0,1),
(0,0,1),
E(1,1, ),F(
),F( ,1,1),
,1,1),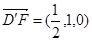 ,
,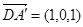 ,
,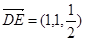 ,
, 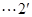
设平面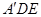 的法向量为
的法向量为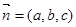 ,
,
则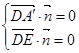 即
即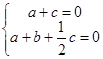
从而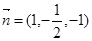
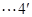
 ,
,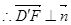
所以
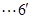
(2)解:设平面ADE的法向量为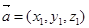 ,
,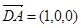 ,
,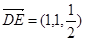
则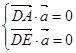 即
即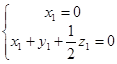 从而
从而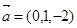
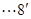
由(1)知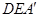 的法向量为
的法向量为 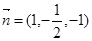
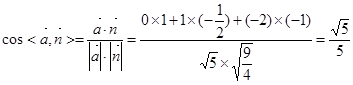
 二面角
二面角 的余弦值为
的余弦值为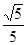 .
. 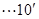
考点:线面垂直以及二面角的平面角
点评:解决的关键是能够合理的建立空间直角坐标系,然后借助于平面的法向量以及直线的方向向量来得到垂直的证明,以及二面角的平面角的求解,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
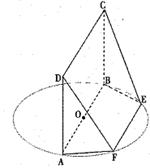
 的底面
的底面 为菱 形 ,AC∩BD=O侧棱
为菱 形 ,AC∩BD=O侧棱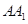 ⊥BD,点F为
⊥BD,点F为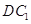 的中点.
的中点.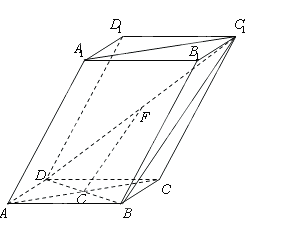
 平面
平面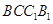 ;
;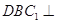 平面
平面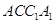 .
.  中.
中.
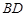 与
与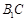 所成的角;
所成的角;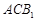
 平面
平面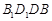 .
.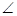 ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.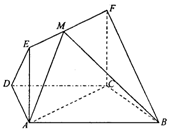
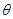 ,求
,求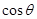 .
. 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.
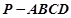 中,侧棱
中,侧棱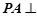 底面
底面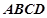 ,底面
,底面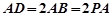 ,
,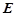 为
为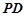 的上一点,且
的上一点,且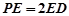 ,
,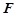 为PC的中点.
为PC的中点.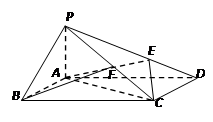

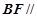 平面AEC;
平面AEC;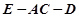 的余弦值.
的余弦值.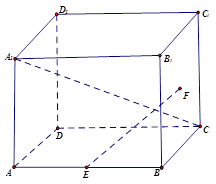
 中,四边形
中,四边形 是菱形,
是菱形,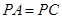 ,
, 为
为 的中点.
的中点.
 面
面 ; (2)求证:平面
; (2)求证:平面 平面
平面 .
.