题目内容
.已知函数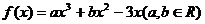 ,在点
,在点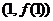 处的切线方程为
处的切线方程为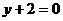 .
.
(Ⅰ)求函数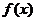 的解析式;
的解析式;
(Ⅱ)若对于区间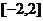 上任意两个自变量的值
上任意两个自变量的值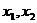 ,都有
,都有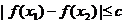 ,求实数
,求实数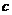 的最小值;
的最小值;
(III)若过点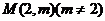 ,可作曲线
,可作曲线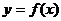 的三条切线,求实数
的三条切线,求实数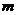 的取值范围.
的取值范围.
【答案】
解:(I)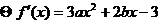 ………………
2分
………………
2分
根据题意,得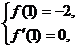 即
即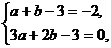
解得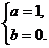
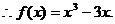 ………………4分
………………4分
(II)令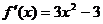
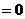 ,解得
,解得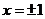
由 ,
,
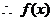 在
在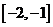 ,
,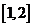 上为增函数,在
上为增函数,在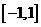 为减函数
为减函数
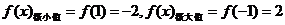 ,又
,又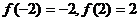
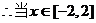 时,
时,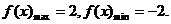 ……………6分
……………6分
则对于区间[-2,2]上任意两个自变量的值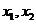 ,都有
,都有

所以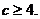 所以的最小值为4。
………………8分
所以的最小值为4。
………………8分
(Ⅲ)设切点为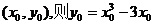
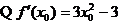 , 切线的斜率为
, 切线的斜率为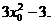 ……………9分
……………9分
则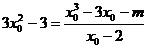 即
即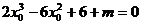 , ……………10分
, ……………10分
因为过点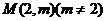 ,可作曲线
,可作曲线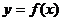 的三条切线
的三条切线
所以方程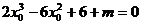 有三个不同的实数解
有三个不同的实数解
即函数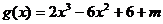 有三个不同的零点,
………………11分
有三个不同的零点,
………………11分
则函数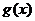 的极大值要大于零且极小值要小于零
的极大值要大于零且极小值要小于零
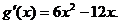
令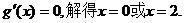
|
|
|
0 |
(0,2) |
2 |
(2,+∞) |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
由上表可知函数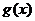 在
在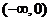 ,(2,+∞)上为增函数,在(0,2)上为减函数,
,(2,+∞)上为增函数,在(0,2)上为减函数,
所以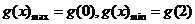 ………………12分
………………12分
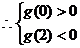 即
即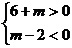 ,∴
,∴ ………………14分
………………14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




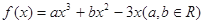 ,在点
,在点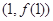 处的切线方程为
处的切线方程为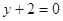 .
.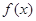 的解析式;
的解析式; 上任意两个自变量的值
上任意两个自变量的值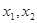 ,都有
,都有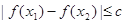 ,求实数
,求实数 的最小值;
的最小值; ,可作曲线
,可作曲线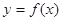 的三条切线,求实数
的三条切线,求实数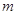 的取值范围.
的取值范围.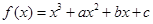 ,曲线
,曲线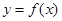 在点
在点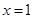 处的切线为
处的切线为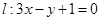 ,若
,若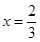 时,
时,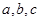 的值;
的值; 上的最大值和最小值.
上的最大值和最小值.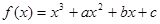 ,曲线
,曲线 在点
在点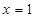 处的切线为
处的切线为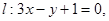 若
若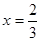 时,
时,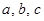 的值;
的值;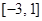 上的最大值和最小值.
上的最大值和最小值. ,在点
,在点 处的切线方程是
处的切线方程是 (e为自然对数的底)。
(e为自然对数的底)。 的值及
的值及 的解析式;
的解析式; 是正数,设
是正数,设 ,求
,求 的最小值;
的最小值; 对一切
对一切 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围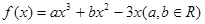 ,在点
,在点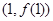 处的切线方程为
处的切线方程为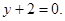
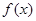 的解析式;
的解析式;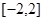 上任意两个自变量的值
上任意两个自变量的值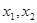 ,都有
,都有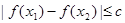 ,求实数
,求实数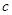 的最小值。
的最小值。 ,可作曲线
,可作曲线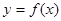 的三条切线,求实数
的三条切线,求实数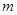 的取值范围。
的取值范围。