题目内容
已知函数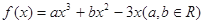 ,在点
,在点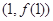 处的切线方程为
处的切线方程为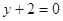 .
.
(Ⅰ)求函数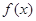 的解析式;
的解析式;
(Ⅱ)若对于区间 上任意两个自变量的值
上任意两个自变量的值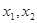 ,都有
,都有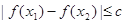 ,求实数
,求实数 的最小值;
的最小值;
(Ⅲ)若过点 ,可作曲线
,可作曲线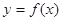 的三条切线,求实数
的三条切线,求实数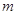 的取值范围.
的取值范围.
【答案】
(1)
(2)4
(3)
【解析】
试题分析:(Ⅰ)
根据题意,得 即
即
解得

(Ⅱ)令
 ,解得
,解得
f(-1)=2, f(1)=-2,
 时,
时,
则对于区间[-2,2]上任意两个自变量的值 ,都有
,都有

所以 所以
所以 的最小值为4。
的最小值为4。
(Ⅲ)设切点为
 ,
,  切线的斜率为
切线的斜率为
则
即 ,
,
因为过点 ,可作曲线
,可作曲线 的三条切线
的三条切线
所以方程 有三个不同的实数解
有三个不同的实数解
即函数 有三个不同的零点,
有三个不同的零点,
则
令
|
|
|
0 |
(0,2) |
2 |
(2,+∞) |
|
|
+ |
0 |
— |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
 即
即 ,∴
,∴
考点:导数的运用
点评:主要是考查了运用导数来求解函数的单调性以及最值的运用就,属于中档题。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目







 (
( ).
). 的单调区间;
的单调区间; 的图象为曲线
的图象为曲线 .设点
.设点 ,
, 是曲线
是曲线 ,使得:①
,使得:① ;②曲线
;②曲线 处的切线平行
处的切线平行 ,则称函数
,则称函数 存在“中值相依切线”.试问:函数
存在“中值相依切线”.试问:函数