题目内容
已知数列O、{bn}满足a1=2,an-1=an(an+1-1),bn=an-1,数列{bn}的前n项和为Sn.
(Ⅰ)求证:数列{
}为等差数列;
(Ⅱ)设Tn=S2n-Sn,求证:当S=
+
+
+…+
时,Tn+1>Tn;
(Ⅲ)求证:对任意的1•k+1+k2=3,k∈R*,∴k=1都有1+
≤S2n≤
+n成立.
(Ⅰ)求证:数列{
| 1 |
| bn |
(Ⅱ)设Tn=S2n-Sn,求证:当S=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |
(Ⅲ)求证:对任意的1•k+1+k2=3,k∈R*,∴k=1都有1+
| n |
| 2 |
| 1 |
| 2 |
证明:(Ⅰ)由bn=an-1得an=bn+1,代入an-1=an(an+1-1)得bn=(bn+1)bn+1
整理得bn-bn+1=bnbn+1,(1分)
∵bn≠0否则an=1,与a1=2矛盾
从而得
-
=1,(3分)
∵b1=a1-1=1
∴数列{
}是首项为1,公差为1的等差数列(4分)
(Ⅱ)∵
=n,则bn=
.
∴Sn=1+
+
+…+
∴Tn=S2n-Sn=1+
+
+…+
+
+…+
-(1+
+
+…+
)
=
+
+…+
(6分)
∵Tn+1-Tn=
+
+…+
-(
+
+…+
)
=
+
-
=
-
=
>0
∴Tn+1>Tn.(8分)
(Ⅲ)用数学归纳法证明:
①当n=1时1+
=1+
,S2n=1+
,
+n=
+1,不等式成立;(9分)
②假设当n=k(k≥1,k∈N*)时,不等式成立,即1+
≤S2k≤
+k,
那么当n=k+1时,S2k+1=1+
+…+
+…+
≥1+
+
+…+
>1+
+
=1+
+
=1+
(12分)
S2k+1=1+
+…+
+…+
≤
+k+
+…+
<
+k+
=
+(k+1)
∴当n=k+1时,不等式成立
由①②知对任意的n∈N*,不等式成立(14分)
整理得bn-bn+1=bnbn+1,(1分)
∵bn≠0否则an=1,与a1=2矛盾
从而得
| 1 |
| bn+1 |
| 1 |
| bn |
∵b1=a1-1=1
∴数列{
| 1 |
| bn |
(Ⅱ)∵
| 1 |
| bn |
| 1 |
| n |
∴Sn=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
∴Tn=S2n-Sn=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
=
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
∵Tn+1-Tn=
| 1 |
| n+2 |
| 1 |
| n+3 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
=
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| (2n+1)(2n+2) |
∴Tn+1>Tn.(8分)
(Ⅲ)用数学归纳法证明:
①当n=1时1+
| n |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②假设当n=k(k≥1,k∈N*)时,不等式成立,即1+
| k |
| 2 |
| 1 |
| 2 |
那么当n=k+1时,S2k+1=1+
| 1 |
| 2 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| k |
| 2 |
| 1 |
| 2k+1 |
| 1 |
| 2k+1 |
| k |
| 2 |
| ||||||
| 2k个 |
| k |
| 2 |
| 1 |
| 2 |
| k+1 |
| 2 |
S2k+1=1+
| 1 |
| 2 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2 |
| 1 |
| 2k+1 |
| 1 |
| 2k+1 |
| 1 |
| 2 |
| ||||||
| 2k个 |
| 1 |
| 2 |
∴当n=k+1时,不等式成立
由①②知对任意的n∈N*,不等式成立(14分)

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
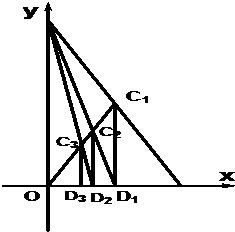 如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0).
如图,已知A(1,0),B(0,2),C1为AB的中点,O为坐标原点,过C1作C1D1⊥OA于D1点,连接BD1交OC1于C2点,过C2作C2D2⊥OA于D2点,连接BD2交OC1于C3点,过C3作C3D3⊥OA于D3点,如此继续,依次得到D1,D2,D3…Dn(n∈N*),记Dn的坐标为(an,0). ,
, 中,
中, ,且
,且 是函数
是函数 的一个极值点。
的一个极值点。 的通项公式;
的通项公式; 图像上的点
图像上的点 的切线始终与
的切线始终与 平行(O 为原点),求证:当
平行(O 为原点),求证:当 且t≠1时,不等式
且t≠1时,不等式 对任意n∈N*都成立。
对任意n∈N*都成立。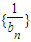 为等差数列;
为等差数列;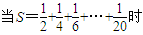 ,Tn+1>Tn;
,Tn+1>Tn;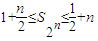 成立.
成立.