Question

10．如图，点A（-1，0）、B（1，0），点C在x轴正半轴上，过线段BC的n等分点D_i作与BC垂直的射线l_i，在l_i上的动点P使∠APB取得最大值的位置记作P_i（i=1，2，3，…，n-1）．是否存在一条圆锥曲线，对任意的正整数n≥2，点P_i（i=1，2，…，n-1）都在这条曲线上？说明理由．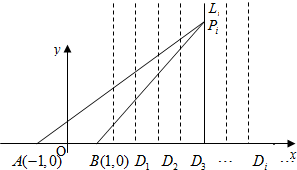

Answer 1

分析 设|BC|=b，P（x，y），则x＞1，y＞0，$x=\frac{i}{n}b$，∠APB=∠PBC-∠PAC$tan∠PAC=\frac{y}{x+1}$，$tan∠PBC=\frac{y}{x-1}$
所以$tan∠APB=\frac{{\frac{y}{x-1}-\frac{y}{x+1}}}{{1+\frac{y^2}{（x-1）（x+1）}}}$=$\frac{2}{{\frac{（x-1）（x+1）}{y}+y}}$，根据基本不等式，即可得出结论．

解答 解：存在一条双曲线，对任意的正整数n≥2，点P_i（i=1，2，…，n-1）都在这条双曲线上．   
如图所示，A（-1，0），B（1，0），设|BC|=b，P（x，y），则x＞1，y＞0，$x=\frac{i}{n}b$，∠APB=∠PBC-∠PAC$tan∠PAC=\frac{y}{x+1}$，$tan∠PBC=\frac{y}{x-1}$
所以$tan∠APB=\frac{{\frac{y}{x-1}-\frac{y}{x+1}}}{{1+\frac{y^2}{（x-1）（x+1）}}}$=$\frac{2}{{\frac{（x-1）（x+1）}{y}+y}}$．    
当i=1，2，3，…，n-1一定时，$x=\frac{i}{n}|BC|$为常数
所以$\frac{（x-1）（x+1）}{y}+y$≥2$\sqrt{（x-1）（x+1）}$，此时tan∠APB取得最大值，
当且仅当$\frac{（x-1）（x+1）}{y}=y$时等号成立，
故x²-y²=1，x＞1，y＞0，P_i在一条双曲线上．

点评 本题考查双曲线的方程与性质，考查差角的正切公式，考查学生分析解决问题的能力，属于中档题．