题目内容
已知数列![]() 的首项
的首项![]() 前
前![]() 项和为
项和为![]() ,且
,且![]()
(I)证明:数列![]() 是等比数列;
是等比数列;
(II)令![]() ,求函数
,求函数![]() 在点
在点![]() 处的导数
处的导数![]() ,并比较
,并比较![]() 与
与![]() 的大小.
的大小.
解:由已知![]() ,可得
,可得![]() 两式相减得
两式相减得
![]() 即
即![]() 从而
从而![]() …………4分
…………4分
当![]() 时
时![]() 所以
所以![]() 又
又![]() 所以
所以![]() 从而
从而![]() ……5分
……5分
故总有![]() ,
,![]() 又
又![]() 从而
从而![]() 即数列
即数列![]() 是等比数列;……6分
是等比数列;……6分
(II)由(I)知![]() ,因为
,因为![]() 所以
所以![]()
从而![]() =
=![]()
=![]() -
-![]()
令![]() ,
,![]()
![]()
错位相减得,![]()
![]() ………………10分
………………10分
由上![]() -
-![]() =
=
![]() =12
=12![]() ①
①
当![]() 时,①式=0所以
时,①式=0所以![]() ;
;
当![]() 时,①式=-12
时,①式=-12![]() 所以
所以![]()
当![]() 时,
时,![]() 又由函数
又由函数![]() 可
可![]()
所以![]() 即①
即①![]() 从而
从而![]()
![]()
![]() ……………………14分
……………………14分

练习册系列答案
相关题目
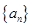 的首项
的首项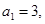 前
前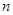 项和为
项和为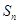 ,且
,且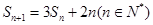 ,
,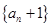 是否成等比数列?并求出数列
是否成等比数列?并求出数列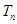 为数列
为数列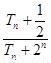 的最小值.
的最小值.