题目内容
10.把下列复数的代数形式化成三角形式和指数形式.(1)z=3$\sqrt{3}$+3i;(2)z=4-4i;(3)z=-6i.
分析 求出各复数的模和辐角可将复数的代数形式化为三角形式
解答 解:(1)z=3$\sqrt{3}$+3i=6($\frac{\sqrt{3}}{2}$+$\frac{1}{2}$i)=6(cos$\frac{π}{6}$+isin$\frac{π}{6}$);
(2)z=4-4i=4$\sqrt{2}$($\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$i)=4$\sqrt{2}$(cos$\frac{7π}{4}$+isin$\frac{7π}{4}$);
(3)z=-6i=6(cos$\frac{3π}{2}$+isin$\frac{3π}{2}$).
点评 本题考查了复数代数形式与三角形式的转化问题,计算出各复数的模和辐角,是解题的关键.

练习册系列答案
相关题目
19.有不少于5个的连续非零自然数的和为2613,则最小的自然数的最大值是( )
| A. | 67 | B. | 78 | C. | 433 | D. | 521 |
10.经过抛物线x2=4y的焦点和双曲线$\frac{{x}^{2}}{17}$-$\frac{{y}^{2}}{8}$=1的右焦点的直线方程为( )
| A. | x+48y-3=0 | B. | x+80y-5=0 | C. | x+3y-3=0 | D. | x+5y-5=0 |
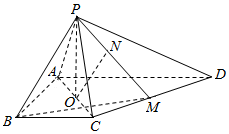 如图,四棱锥P-ABCD,AD∥BC,AD=2BC=4,AB=2$\sqrt{3}$,∠BAD=90°,M,O分别为CD和AC的中点,PO⊥平面ABCD.
如图,四棱锥P-ABCD,AD∥BC,AD=2BC=4,AB=2$\sqrt{3}$,∠BAD=90°,M,O分别为CD和AC的中点,PO⊥平面ABCD.