题目内容
若等腰三角形顶角的正弦值为
,则底角的余弦值为
或
或
.
| 24 |
| 25 |
| 3 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 5 |
分析:设出顶角为α,根据三角形的内角和定理表示出底角,由题意得到sinα的值,由α为三角形的内角,利用同角三角函数间的基本关系求出cosα的值,表示出底角的余弦值,利用诱导公式及二倍角的余弦函数公式化简后,将求出的cosα的值代入即可求出底角的余弦值.
解答:解:设顶角为α,则底角为
=90°-
,
∴sinα=
,又α为三角形的内角,
∴cosα=±
,
当cosα=
时,cos(90°-
)=sin
=
=
,
当cosα=-
时,cos(90°-
)=sin
=
=
.
故答案为:
或
| 180°-α |
| 2 |
| α |
| 2 |
∴sinα=
| 24 |
| 25 |
∴cosα=±
| 7 |
| 25 |
当cosα=
| 7 |
| 25 |
| α |
| 2 |
| α |
| 2 |
|
| 3 |
| 5 |
当cosα=-
| 7 |
| 25 |
| α |
| 2 |
| α |
| 2 |
|
| 4 |
| 5 |
故答案为:
| 3 |
| 5 |
| 4 |
| 5 |
点评:此题考查了同角三角函数间的基本关系,等腰三角形的性质,以及二倍角的余弦函数公式,熟练掌握基本关系是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数
已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)顺次为一次函数 、
、 、…、
、…、 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数 图像上的点,点列
图像上的点,点列 、
、 、…、
、…、 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点 、
、 、
、 构成一个顶角的顶点为
构成一个顶角的顶点为
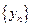 的通项公式,并证明
的通项公式,并证明 为常数,并求出数列
为常数,并求出数列 的通项公式;
的通项公式;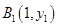 、
、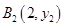 、…、
、…、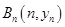 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数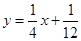 图像上的点,点列
图像上的点,点列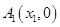 、
、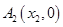 、…、
、…、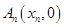 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中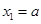 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点 、
、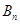 、
、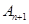 构成一个顶角的顶点为
构成一个顶角的顶点为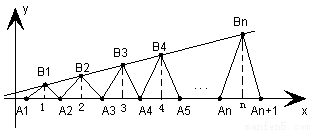
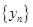 的通项公式,并证明
的通项公式,并证明 为常数,并求出数列
为常数,并求出数列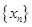 的通项公式;
的通项公式; 图象上的点,点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N)顺次为x轴正半轴上的点,其中x1=a(0<a<1),对于任意n∈N,点An、Bn、An+1构成一个顶角的顶点为Bn的等腰三角形.
图象上的点,点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N)顺次为x轴正半轴上的点,其中x1=a(0<a<1),对于任意n∈N,点An、Bn、An+1构成一个顶角的顶点为Bn的等腰三角形.