题目内容
已知点列B1(1，y1)、B2(2，y2)、…、Bn(n，yn)(n∈N+)顺次为一次函数y＝
x＋
图像上的点，点列A1(x1，0)、A2(x2，0)、…、
(n∈N+)顺次为x轴正半轴上的点，其中x1＝a(0＜a＜1)，对于任意n∈N+，点
构成一个顶角的顶点为Bn的等腰三角形．
(1)求数列{yn}的通项公式，并证明{yn}是等差数列；
(2)证明
为常数，并求出数列{xn}的通项公式；
(3)在上述等腰三角形
中，是否存在直角三角形？若有，求出此时a值；若不存在，请说明理由．
答案：
解析：
解析：
解：(1)
(nÎ
N)，∵
，∴{
}为等差数列
(2)因为
与
为等腰三角形．
所以
，两式相减得
．
∴x1，x3，x5，…，x2n－1及x2，x4，x6，…，x2n都是公差为2的等差数列，
∴
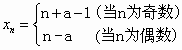
(3)要使AnBnAn+1为直角三角形，则|AnAn+1|＝2
＝2(
)Þ
xn+1－xn＝2()
①当n为奇数时，xn+1＝n＋1－a，xn＝n＋a－1，∴xn+1－xn＝2(1－a)．
Þ
2(1－a)＝2()Þ
a＝
(n为奇数，0＜a＜1)(*)
取n＝1，得a＝
，取n＝3，得a＝
，若n≥5，则(*)无解；
②当n为偶数时，xn+1＝n＋a，xn＝n－a，∴xn+1－xn＝2a．
∴2a＝2()Þ
a＝(n为偶数，0＜a＜1)(*¢
)，
取n＝2，得a＝
，若n≥4，则(*¢
)无解．
综上可知，存在直角三形，此时a的值为、、．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知点列B1（1，y1）、B2（2，y2）、…、Bn（n，yn）（n∈N）顺次为一次函数y=
已知点列B1（1，y1）、B2（2，y2）、…、Bn（n，yn）（n∈N）顺次为一次函数