题目内容
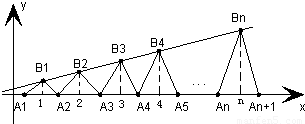
已知点列B1（1，y1）、B2（2，y2）、…、Bn（n，yn）（n∈N）顺次为一次函数
图象上的点，点列A1（x1，0）、A2（x2，0）、…、An（xn，0）（n∈N）顺次为x轴正半轴上的点，其中x1=a（0＜a＜1），对于任意n∈N，点An、Bn、An+1构成一个顶角的顶点为Bn的等腰三角形．（1）求数列{yn}2的通项公式，并证明{yn}3是等差数列；
（2）证明xn+2-xn5为常数，并求出数列{xn}6的通项公式；
（3）问上述等腰三角形An8Bn9An+110中，是否存在直角三角形？若有，求出此时a值；若不存在，请说明理由．
【答案】分析：（1）利用点列B1（1，y1）、B2（2，y2）、…、Bn（n，yn）（n∈N）顺次为一次函数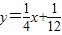
，可得数列{yn}的通项公式，进而有{yn}是等差数列；
（2）根据△AnBnAn+1与△An+1Bn+1An+2为等腰三角形，可得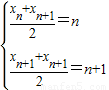
，两式相减，即可求出数列{xn}的通项公式；
（3）要使△AnBnAn+1为直角三角形，则
，根据（2）分n为奇数、偶数时，进行讨论，可求此时a值．
解答：解：（1）∵点列B1（1，y1）、B2（2，y2）、…、Bn（n，yn）（n∈N）顺次为一次函数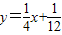
∴
∴
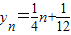
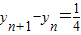
∴{yn}是等差数列；
（2）∵△AnBnAn+1与△An+1Bn+1An+2为等腰三角形
∴
．∴xn+2-xn=2
∴
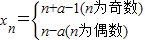
（3）要使△AnBnAn+1为直角三角形，则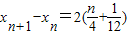
当n为奇数时，xn+1-xn=2（1-a），∴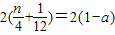
∴
n=1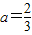，得
，n=3得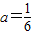
，n≥5，则无解；
当n为偶数时，同理得
n=2，得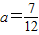
，n≥4，则无解；
∴存在直角三角形，此时a值为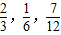
点评：本题以函数为载体，考查数列知识，考查数列的通项，考查分类讨论思想，有较强的综合性．
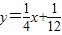，可得数列{yn}的通项公式，进而有{yn}是等差数列；（2）根据△AnBnAn+1与△An+1Bn+1An+2为等腰三角形，可得
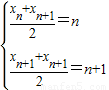，两式相减，即可求出数列{xn}的通项公式；（3）要使△AnBnAn+1为直角三角形，则
，根据（2）分n为奇数、偶数时，进行讨论，可求此时a值．解答：解：（1）∵点列B1（1，y1）、B2（2，y2）、…、Bn（n，yn）（n∈N）顺次为一次函数
∴
∴
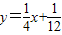
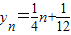
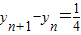
∴{yn}是等差数列；
（2）∵△AnBnAn+1与△An+1Bn+1An+2为等腰三角形
∴
．∴xn+2-xn=2∴
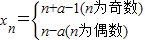
（3）要使△AnBnAn+1为直角三角形，则
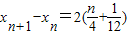
当n为奇数时，xn+1-xn=2（1-a），∴
∴
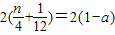
n=1，得
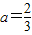，n=3得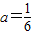，n≥5，则无解；当n为偶数时，同理得
n=2，得
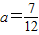，n≥4，则无解；∴存在直角三角形，此时a值为
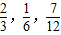
点评：本题以函数为载体，考查数列知识，考查数列的通项，考查分类讨论思想，有较强的综合性．
练习册系列答案
相关题目
已知点列B1（1，y1）、B2（2，y2）、…、Bn（n，yn）（n∈N）顺次为一次函数y=
已知点列B1（1，y1）、B2（2，y2）、…、Bn（n，yn）（n∈N）顺次为一次函数