题目内容
已知点 、
、 ,若动点
,若动点 满足
满足 .
.
(1)求动点 的轨迹
的轨迹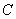 ;
;
(2)在曲线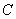 上求一点
上求一点 ,使点
,使点 到直线
到直线 :
: 的距离最小.
的距离最小.
解:(1)设动点 ,又点
,又点 、
、 ,
,
∴ ,
, ,
, . ……… 3分
. ……… 3分
由 ,得
,得 , ……… 4分
, ……… 4分
∴ ,故
,故 ,即
,即 ,
,
∴轨迹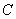 是焦点为
是焦点为 、长轴长
、长轴长 的椭圆; ……… 7分
的椭圆; ……… 7分
评分说明:只求出轨迹方程,没有说明曲线类型或交代不规范的扣 分.
分.
(2)椭圆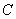 上的点
上的点 到直线
到直线 的距离的最值等于平行于直线
的距离的最值等于平行于直线 :
:
且与椭圆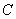 相切的直线
相切的直线 与直线
与直线 的距离.
的距离.
设直线 的方程为
的方程为 . ……… 8分
. ……… 8分
由 ,消去
,消去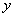 得
得 (*).
(*).
依题意得 ,即
,即 ,故
,故 ,解得
,解得 .
.
当 时,直线
时,直线 :
: ,直线
,直线 与
与 的距离
的距离 .
.
当 时,直线
时,直线 :
: ,直线
,直线 与
与 的距离
的距离 .
.
由于 ,故曲线
,故曲线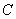 上的点
上的点 到直线
到直线 的距离的最小值为
的距离的最小值为 .…12分
.…12分
当 时,方程(*)化为
时,方程(*)化为 ,即
,即 ,解得
,解得 .
.
由 ,得
,得 ,故
,故 . ……… 13分
. ……… 13分
∴曲线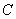 上的点
上的点 到直线
到直线 的距离最小. ……… 14分
的距离最小. ……… 14分

练习册系列答案
相关题目
 ,其中
,其中 、
、
 ,
, 是虚数单位,则
是虚数单位,则
 图像上,
图像上, ,则下列点也在此图像上的是
,则下列点也在此图像上的是 B. (10a,1
B. (10a,1 b) C.
b) C.  D.
D. 
 等于 ( )
等于 ( )  B.
B.  C.
C.  D.
D.
 的值的一个程序框图,其中判断框内应填入的条
的值的一个程序框图,其中判断框内应填入的条 ___?
___?
 的定义域为
的定义域为 ,那么其值域为 ( )
,那么其值域为 ( ) B.
B. D.
D.
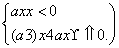 满足对任意x1≠x2,都有
满足对任意x1≠x2,都有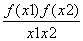 >0成立,则a的取值范围是
>0成立,则a的取值范围是 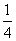 ] D.(3, +∞)
] D.(3, +∞) 中,
中, ,则此数列前13项的和为( )
,则此数列前13项的和为( ) 满足
满足 是虚数单位),则
是虚数单位),则