题目内容
(本题满分14分)已知顶点在原点, 焦点在x轴上的抛物线被直线y=2x+1截得的弦长为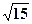 ,求抛物线的方程.
,求抛物线的方程.
解:依题意可设抛物线方程为: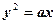 (a可正可负),与直线y=2x+1截得的弦为AB;
(a可正可负),与直线y=2x+1截得的弦为AB;
则可设A(x1,y1)、B(x2,y2)联立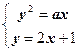 得
得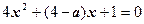
即: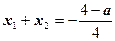
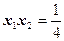 (6分)
(6分)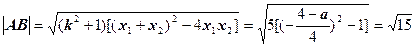
得:a=12或-4(6分)
所以抛物线方程为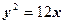 或
或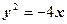 (2分)
(2分)
解析

练习册系列答案
相关题目
已知曲线M与曲线N:ρ=5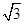 cosθ-5sinθ关于极轴对称,则曲线M的方程为( )
cosθ-5sinθ关于极轴对称,则曲线M的方程为( )
A.ρ=-10cos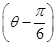 | B.ρ=10cos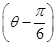 |
C.ρ=-10cos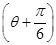 | D.ρ=10cos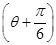 |
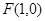 ,直线
,直线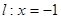 ,
,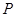 为平面上的动点,过
为平面上的动点,过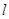 的垂线,垂足为点
的垂线,垂足为点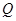 ,且
,且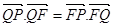 .
.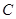 的方程;
的方程;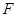 的直线交轨迹
的直线交轨迹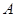 ,
,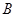 两点,交直线
两点,交直线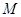 ,已知
,已知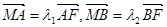 ,求
,求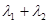 的值.
的值.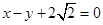 的距离为3。
的距离为3。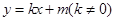 与椭圆相交于不同的两点M,N,当|AM|=|AN|时,求m的取值范围.
与椭圆相交于不同的两点M,N,当|AM|=|AN|时,求m的取值范围.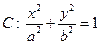 (
(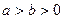 )的一个焦点坐标为
)的一个焦点坐标为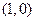 ,且长轴长是短轴长的
,且长轴长是短轴长的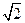 倍.
倍.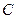 的方程;
的方程; 为坐标原点,椭圆
为坐标原点,椭圆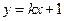 相交于两个不同的点
相交于两个不同的点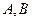 ,线段
,线段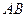 的中点为
的中点为 ,若直线
,若直线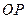 的斜率为
的斜率为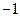 ,求△
,求△ 的面积.
的面积.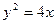 ,过点
,过点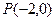 的直线AB交抛物线于点
的直线AB交抛物线于点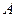 、
、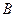 ,若线段
,若线段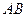 的垂直平分线交
的垂直平分线交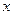 轴于点
轴于点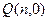 ,求
,求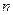 的取值范围.
的取值范围.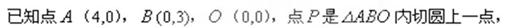
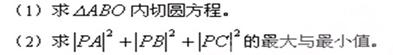
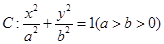 上的任意一点到它两个焦点
上的任意一点到它两个焦点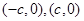 的距离之和为
的距离之和为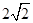 ,且它的焦距为2.
,且它的焦距为2.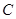 的方程;
的方程;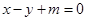 与椭圆
与椭圆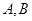 ,且线段
,且线段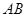 的中点
的中点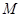 不在圆
不在圆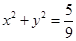 内,求实数
内,求实数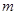 的取值范围.
的取值范围. 是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有
是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有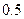 米的距离,现有一货车,车宽
米的距离,现有一货车,车宽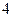 米,车高
米,车高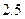 米.
米.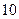 米,则应如何设计隧道才能保证此货车正常通行?
米,则应如何设计隧道才能保证此货车正常通行?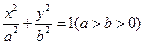 的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?