题目内容
14．函数$f（x）=arcsin（{\frac{x}{3}-1}）$的定义域为[0，6]．分析 设t=$\frac{x}{3}$-1，根据反正弦函数的定义域解关于x的不等式-1≤$\frac{x}{3}$-1≤1，即可得出f（x）的定义域．
解答 解：设t=$\frac{x}{3}$-1，
∵反正弦函数y=arcsint的定义域为[-1，1]，
∴解不等式-1≤$\frac{x}{3}$-1≤1，可得x∈[0，6]．
所以函数的定义域为：[0，6]．
故答案为：[0，6]．
点评 本题考查反三角函数的定义域的求法，基本知识的考查．
练习册系列答案
考前必练系列答案
相关题目
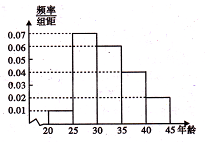某市为增强市民的环境保护意识，面向全市征召义务宣传志愿者．把符合条件的1000名志愿者按年龄分组：第1组[20，25）、第2组[25，30）、第3组[30，35）、第4组[35，40）、第5组[40，45），得到的频率分布直方图如图所示：
6．方程$sinx=\frac{1}{2}$的解为（ ）
| A． | $x=kπ+{（-1）}^{k}•\frac{π}{6}$，k∈Z | B． | $x=2kπ{（{-1}）^k}•\frac{π}{6}$，k∈Z* | ||
| C． | $x=kπ+{（{-1}）^{k+1}}•\frac{π}{6}$，k∈Z | D． | $x=2kπ+{（{-1}）^{k+1}}•\frac{π}{6}$，k∈Z |