题目内容
不等式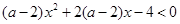 对一切
对一切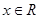 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )
A.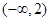 | B.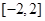 | C.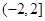 | D.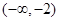 |
C
解析试题分析:当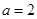 时,原不等式即为-4<0,恒成立,
时,原不等式即为-4<0,恒成立,
即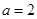 满足条件;
满足条件;
当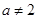 时,要使不等式
时,要使不等式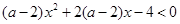 对一切x∈R恒成立,
对一切x∈R恒成立,
必须 <0, △=
<0, △= ,故有
,故有
,解得,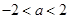
综上所述, 的取值范围是
的取值范围是 ,故选C
,故选C
考点:二次函数的性质
点评:本题考查二次函数的性质,易错点在于忽略a-2=0这种情况而导致错误,属于中档题.

练习册系列答案
相关题目
函数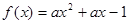 在
在 上满足
上满足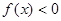 ,则
,则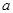 的取值范围是( )
的取值范围是( )
A.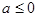 | B.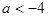 | C.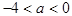 | D.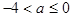 |
设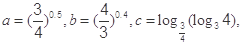 则( ).
则( ).
A.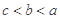 | B.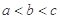 | C.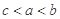 | D.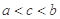 |
不等式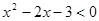 的解集为
的解集为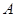 ,不等式
,不等式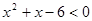 的解集为
的解集为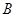 ,不等式
,不等式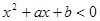 的解集是
的解集是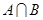 ,那么
,那么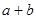 等于 ( )
等于 ( )
| A.-3 | B.1 | C.-1 | D.3 |
设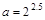 ,
,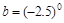 ,
,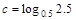 ,则
,则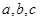 的大小关系是( )
的大小关系是( )
A.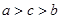 | B.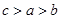 | C.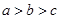 | D.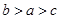 |
若不等式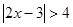 与不等式
与不等式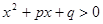 的解集相同,则p:q等于 ( )
的解集相同,则p:q等于 ( )
| A.12:7 | B.7:12 | C.-12:7 | D.-3 :4 |
对任意的实数 ,不等式
,不等式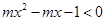 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是
A.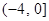 | B.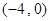 | C.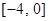 | D.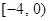 |
若2-m与|m|-3同号,则m的取值范围是 ( )
| A.(3,+∞) | B.(-3,3) |
| C.(2,3)∪(-∞,-3) | D.(-3,2)∪(3,+∞) |
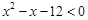 的解集为________.
的解集为________.