题目内容
15.在△ABC中,角A,B,C所对的边分别为a,b,c,若c2=(a+b)2-6,C=60°,则△ABC的面积是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | 3$\sqrt{3}$ |
分析 利用余弦定理可得ab,再利用三角形面积计算公式即可得出.
解答 解:∵c2=(a+b)2-6=a2+b2+2ab-6,c2=a2+b2-2abcos60°,
∴a2+b2+2ab-6=a2+b2-ab,
∴ab=2.
∴S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}×2×sin6{0}^{°}$=$\frac{\sqrt{3}}{2}$.
故选:A.
点评 本题考查了余弦定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知集合A={x|x2-x<2},B={x||x+1|<1},则A∩(∁RB)=( )
| A. | (-1,0) | B. | (-1,0] | C. | (0,2) | D. | [0,2) |
5.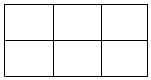 从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )
从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )
 从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )
从6个正方形拼成的12个顶点(如图)中任取3个顶点作为一组,其中可以构成三角形的组数为( )| A. | 208 | B. | 204 | C. | 200 | D. | 196 |