题目内容
已知△ABC的面积为3,设
和
的夹角为θ.
(1)若
•
=6,求θ的值;
(2)若
≤θ≤
,求函数f(θ)=2sin2(
+θ)-
cos2θ的最大值及此时θ的值.
| AB |
| AC |
(1)若
| AB |
| AC |
(2)若
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3 |
考点:三角函数的最值,平面向量数量积的运算,数量积表示两个向量的夹角
专题:三角函数的求值,解三角形
分析:(1)由三角形的面积公式和向量的夹角公式,得到方程组,解得即可.
(2)利用倍角公式和正弦函数的和差公式,计算即可.
(2)利用倍角公式和正弦函数的和差公式,计算即可.
解答:
解:(1)由已知得,
,
解得tanθ=1,又θ∈[0,π],
故θ=
,
(2)∵f(θ)=2sin2(
+θ)-
cos2θ=1-cos[2(
+θ)]-
cos2θ=sin2θ-
cos2θ+1=2sin(2θ-
),
∵
≤θ≤
,
∴
≤2θ-
≤
π,
当2θ-
=
,即θ=
时,f(θ)max=3,
|
解得tanθ=1,又θ∈[0,π],
故θ=
| π |
| 4 |
(2)∵f(θ)=2sin2(
| π |
| 4 |
| 3 |
| π |
| 4 |
| 3 |
| 3 |
| π |
| 3 |
∵
| π |
| 4 |
| π |
| 2 |
∴
| π |
| 6 |
| π |
| 3 |
| 2 |
| 3 |
当2θ-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
点评:本题主要考查了向量的夹角公式,以及三角函数最值问题,属于基础题.

练习册系列答案
相关题目
 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD=a,M、N分别是AB、PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AD=a,M、N分别是AB、PC的中点.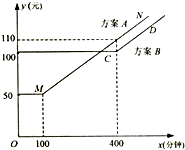 移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等).
移动公司根据市场客户的不同需求,对某地区的手机套餐通话费提出两种优惠方案,两种方案所付电话费(元)与通话时间(分钟)之间的关系如图所示(实线部分:MN与CD平行即直线方程y=kx+b中的斜率k相等).