题目内容
20.已知抛物线y2=4x,过其焦点F作直线l交抛物线于A,B两点,M为抛物线的准线与x轴的交点,tan∠AMB=$\frac{4}{3}$,则|AB|=( )| A. | 4 | B. | 8 | C. | 16 | D. | 18 |
分析 设AB方程y=k(x-1),与抛物线方程y2=4x联立,利用tan∠AMB=$\frac{4}{3}$,建立k的方程,求出k,即可得出结论.
解答 解:焦点F(1,0),M(-1,0),设AB方程y=k(x-1),
设A(x1,y1),B(x2,y2)
∵tan∠AMB=$\frac{4}{3}$,
∴$\frac{\frac{{y}_{1}}{{x}_{1}+1}-\frac{{y}_{2}}{{x}_{2}+1}}{1+\frac{{y}_{1}}{{x}_{1}+1}•\frac{{y}_{2}}{{x}_{2}+1}}$=$\frac{4}{3}$,
整理可得2k(x1-x2)=$\frac{4}{3}$(x1+1)(x2+1)+$\frac{4}{3}$y1y2…(*)
y=k(x-1),与y2=4x联立可得k2x2-(2k2+4)x+k2=0
可得x1x2=1,x1+x2=$\frac{4}{{k}^{2}}$+2,y1y2=-4
代入(*)可得2k(x1-x2)=$\frac{4}{3}$•$\frac{4}{{k}^{2}}$,∴x1-x2=$\frac{8}{3{k}^{3}}$,
∴($\frac{4}{{k}^{2}}$+2)2-4=($\frac{8}{3{k}^{3}}$)2,
∴k=±$\frac{\sqrt{3}}{3}$,
∴x1+x2=$\frac{4}{{k}^{2}}$+2=14,
∴|AB|=$\sqrt{1+\frac{1}{3}}•\sqrt{196-4}$=16.
故选:C.
点评 本题考查直线与抛物线的位置关系,考查差角的正切公式,正确运用韦达定理是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8.过抛物线y2=2px(p>0)的焦点F,且倾斜角为$\frac{π}{4}$的直线与抛物线交于A,B两点,若AB的垂直平分线经过点(0,2),M为抛物线上的一个动点,则M到直线11:5x-4y+4=0和l2:x=-$\frac{2}{5}$的距离之和的最小值为( )
| A. | $\frac{6\sqrt{41}}{41}$ | B. | $\frac{6\sqrt{31}}{31}$ | C. | $\frac{3\sqrt{41}}{41}$ | D. | $\frac{3\sqrt{31}}{31}$ |
15.已知抛物线C:y2=4x,直线l交C于A,B两点,O为坐标原点,直线OA,OB的斜率分别为k1,k2,若k1•k2=-2,则△AOB面积的最小值为( )
| A. | 4 | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
5.设α、β、γ是不同的平面,m,n是不同的直线,则由下列条件能得出m⊥β的是( )
| A. | n⊥α,n⊥β,m⊥α | B. | α∩β=m,α⊥β,β⊥γ | C. | m⊥n,n?β | D. | α⊥β,α∩β=n,m⊥n |
10.sin$\frac{17π}{3}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
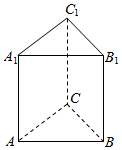 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=AC=2,AA1=4
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=AC=2,AA1=4