题目内容
(本小题满分14分)已知奇函数
(1)求实数m的值,并在给出的直角坐标系中画出 的图象;
的图象;
(2)若函数f(x)在区间[-1,a-2]上单调递增,试确定a的取值范围
【解析】
试题分析:解决本题的关键是要理解具有奇偶性的分段函数的解析式的求解方法,再有注意函数的单调区间的子区间都是单调的.
试题解析:(1)当 时,
时, ,
,
又 为奇函数,∴
为奇函数,∴ ,∴
,∴ ,
,
∴ 4分
4分
y=f(x)的图象如右所示

(2)由(1)知f(x)= , 8分
, 8分
由图象可知, 在[-1,1]上单调递增,要使
在[-1,1]上单调递增,要使 在[-1,|a|-2]上单调递增,只需
在[-1,|a|-2]上单调递增,只需 10分
10分
解之得 12分
12分
考点:应用奇函数的定义确定函数解析式中的参数问题,画函数图像的基本功,函数单调区间的确定.

练习册系列答案
相关题目
若函数y=ax-x-a有两个零点,则a的取值范围是( )
| A、(1,+∞) | B、(0,1) |
| C、(0,+∞) | D、∅ |
 ,给出下列四个结论:
,给出下列四个结论: 是椭圆;
是椭圆;  轴对称;
轴对称; 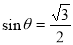 ”是“
”是“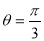 ”的( )
”的( ) 的图象,则
的图象,则 与
与 的大小关系是 ( )
的大小关系是 ( )

 与
与 的各组函数中,表示相等函数的是 ( )
的各组函数中,表示相等函数的是 ( )
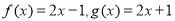
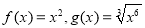
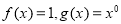
 ,且
,且 ,则实数
,则实数 的值为___ .
的值为___ . 中,若
中,若 ,则
,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.
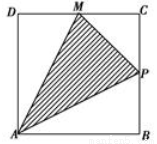
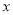 为自变量,三角形APM的面积函数的图像形状大致是图中的( )
为自变量,三角形APM的面积函数的图像形状大致是图中的( )