题目内容
已知椭圆 的离心率为
的离心率为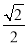 ,且过点
,且过点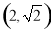
(1)求椭圆的标准方程:
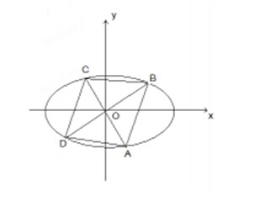 (2)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,若
(2)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,若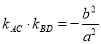
①求 的最值:
的最值:
②求证:四边形ABCD的面积为定值.
(1) ;(2)①
;(2)① 的最小值为
的最小值为 ,最大值为
,最大值为 ;②
;② .
.
【解析】
试题分析:(1)根据离心率写出有关 的等式,将点
的等式,将点 代入椭圆方程,同时椭圆中
代入椭圆方程,同时椭圆中 三个等式联立求得
三个等式联立求得 的值,得到所求椭圆的方程;(2)①直线
的值,得到所求椭圆的方程;(2)①直线 的斜率存在时
的斜率存在时 与(1)中的椭圆方程联立,又韦达定理得到
与(1)中的椭圆方程联立,又韦达定理得到 ,同时又得到
,同时又得到 ,
, 化简得到关于
化简得到关于 和
和 的关系
的关系 ,所以要求的
,所以要求的 ,根据函数单调性求得
,根据函数单调性求得 ;当直线
;当直线 的斜率不存在时得到
的斜率不存在时得到 ,综上得到
,综上得到 的最小值为
的最小值为 ,最大值为
,最大值为 ;②根据已知条件及椭圆的对称性知
;②根据已知条件及椭圆的对称性知 ,由弦长公式及点到直线的距离公式,得到
,由弦长公式及点到直线的距离公式,得到 ,进而得到四边形的
,进而得到四边形的 面积为定值
面积为定值 .
.
试题解析: ;
;
(2)设




 ,
,


 .
.
考点:1.椭圆的标准方程;2.韦达定理;3.弦长公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数y=ax-x-a有两个零点,则a的取值范围是( )
| A、(1,+∞) | B、(0,1) |
| C、(0,+∞) | D、∅ |
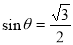 ”是“
”是“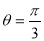 ”的( )
”的( ) 中,若
中,若 ,则
,则 的值是( )
的值是( ) B.
B. C.
C. D.
D.
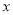 为自变量,三角形APM的面积函数的图像形状大致是图中的( )
为自变量,三角形APM的面积函数的图像形状大致是图中的( )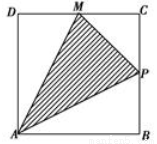

 的定义域为
的定义域为 ,则函数
,则函数 的定义域为( )
的定义域为( ) B.
B.  C.
C.  D.
D. 
 : “方程
: “方程 表示双曲线” (
表示双曲线” ( );命题
);命题 :
: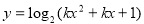 定义域为
定义域为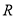 ,若命题
,若命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数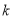 的取值范围.
的取值范围. 的左、右焦点分别为
的左、右焦点分别为 ,以
,以 为圆心,
为圆心, (
( 为椭圆中心)为半径作圆
为椭圆中心)为半径作圆 ,且
,且 恰好为圆
恰好为圆 B.
B. C.
C. D.
D.