题目内容
10.设函数$f(x)=\frac{{\sqrt{3}}}{2}sinx+\frac{1}{2}cosx$,若将函数f(x)的图象向右平移$\frac{π}{6}$个单位,所得图象对应函数为y=g(x),则( )| A. | y=g(x)的图象关于直线$x=-\frac{π}{3}$对称 | B. | y=g(x)图象关于原点对称 | ||
| C. | y=g(x)的图象关于点$({-\frac{π}{3},0})$对称 | D. | y=g(x)图象关于y轴对称 |
分析 根据三角函数的图象平移关系进行求解即可.
解答 解:$f(x)=\frac{{\sqrt{3}}}{2}sinx+\frac{1}{2}cosx$=sin(x+$\frac{π}{6}$),
将函数f(x)的图象向右平移$\frac{π}{6}$个单位,所得图象对应函数为y=g(x),
则g(x)=f(x-$\frac{π}{6}$)=sin(x+$\frac{π}{6}$-$\frac{π}{6}$)=sinx,
此时函数g(x)为奇函数,图象关于原点对称,
故选:B.
点评 本题主要考查三角函数的图象变换关系,利用辅助角公式将函数进行化简是解决本题的关键.

练习册系列答案
相关题目
1.以下是程序框图的基本逻辑结构,顺序正确的是( )
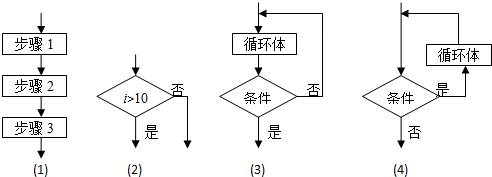

| A. | (1)是顺序结构(2)是条件结构(3)是当型循环结构(4)是直到型循环结构 | |
| B. | (1)是条件结构(2)是顺序结构(3)是当型循环结构(4)是直到型循环结构 | |
| C. | (1)是顺序结构(2)是条件结构(3)是直到型循环结构(4)是当型循环结构 | |
| D. | (1)是顺序结构(2)是当型循环结构(3)是条件结构(4)是直到型循环结构 |
15.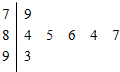 在广雅中学“十佳学生”评选的演讲比赛中,如图是七位评委为某学生打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
在广雅中学“十佳学生”评选的演讲比赛中,如图是七位评委为某学生打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
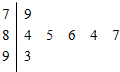 在广雅中学“十佳学生”评选的演讲比赛中,如图是七位评委为某学生打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
在广雅中学“十佳学生”评选的演讲比赛中,如图是七位评委为某学生打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )| A. | 85,85 | B. | 84,86 | C. | 84,85 | D. | 85,86 |
2.对于向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$和实数λ,下列正确的是( )
| A. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=0,则$\overrightarrow{a}$=0或$\overrightarrow{b}$=0 | B. | 若λ$\overrightarrow{a}$=0,则λ=0或$\overrightarrow{a}$=$\overrightarrow{0}$ | ||
| C. | 若$\overrightarrow{a}$2=$\overrightarrow{b}$2,则$\overrightarrow{a}$=$\overrightarrow{b}$或$\overrightarrow{a}$=-$\overrightarrow{b}$ | D. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$ |
 正三角形ABC的边长为2,将它沿高AD翻折,使BD⊥CD,此时四面体ABCD外接球表面积为5π.
正三角形ABC的边长为2,将它沿高AD翻折,使BD⊥CD,此时四面体ABCD外接球表面积为5π.