题目内容
【题目】已知 ![]() ,分别是椭圆
,分别是椭圆 ![]() 的左、右焦点.
的左、右焦点.
(1)若点 ![]() 是第一象限内椭圆上的一点,
是第一象限内椭圆上的一点, ![]() ,求点
,求点 ![]() 的坐标;
的坐标;
(2)设过定点 ![]() 的直线
的直线 ![]() 与椭圆交于不同的两点
与椭圆交于不同的两点 ![]() ,且
,且 ![]() 为锐角(其中
为锐角(其中 ![]() 为坐标原点),求直线
为坐标原点),求直线 ![]() 的斜率
的斜率 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:易知 ![]() .
.![]() ,设
,设 ![]() ,则
,则![]() ,又
,又 ![]() .
.
联立 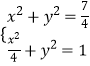 ,解得
,解得 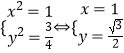 ,故
,故 ![]()
(2)解:显然 ![]() 不满足题设条件,可设
不满足题设条件,可设 ![]() 的方程为
的方程为 ![]() ,
,
设 ![]() ,
,
联立 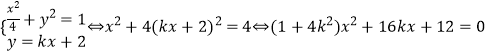
![]()
由 ![]()
![]() ,得
,得 ![]() .①
.①
又 ![]() 为锐角
为锐角 ![]() ,
,![]()
又 ![]()
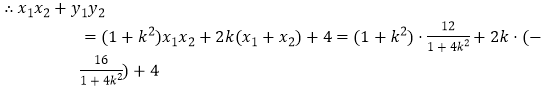
![]() .②
.②
综①②可知 ![]() 的取值范围是
的取值范围是 ![]()
【解析】(1)根据题目中所给的条件的特点,求得椭圆的a,b,c,可得左右焦点,设P(x,y)(x>0,y>0),运用向量的数量积的坐标表示,解方程可得P的坐标;
(2)设过定点M(0,2)的直线l方程为y=kx+2,A(x1 , y1),B(x2 , y2),与椭圆联立,注意到交于不同的两点A、B,△>0且∠AOB为锐角(其中O为作标原点),利用韦达定理,代入化简,求直线l的斜率k的取值范围.

练习册系列答案
相关题目