题目内容
已知直线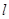 经过抛物线
经过抛物线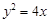 的焦点F,且与抛物线相交于A、B两点.
的焦点F,且与抛物线相交于A、B两点.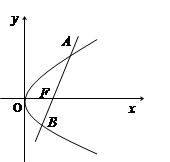
(1)若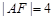 ,求点A的坐标;
,求点A的坐标;
(2)若直线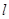 的倾斜角为
的倾斜角为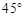 ,求线段AB的长.
,求线段AB的长.
(1) 点A的坐标为 或
或 . (2) 线段AB的长是8
. (2) 线段AB的长是8
解析试题分析:解:由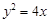 ,得
,得 ,其准线方程为
,其准线方程为 ,焦点
,焦点 .
.
设 ,
, .
.
(1)由抛物线的定义可知,  ,从而
,从而 .
.
代入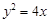 ,解得
,解得 .
.
∴ 点A的坐标为 或
或 .
.
(2)直线l的方程为 ,即
,即 .
.
与抛物线方程联立,得 ,
,
消y,整理得 ,其两根为
,其两根为 ,且
,且 .
.
由抛物线的定义可知,  .
.
所以,线段AB的长是8.
考点:直线与抛物线的位置关系
点评:解决的关键是利用抛物线的定义以及直线与抛物线的位置关系联立方程组来结合韦达定理得到,属于基础题。

练习册系列答案
相关题目
 的参数方程为
的参数方程为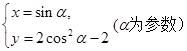 ,曲线
,曲线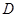 的极坐标方程为
的极坐标方程为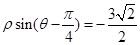 .
. 的直线
的直线 交直线
交直线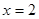 于
于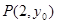 ,过点
,过点 的直线
的直线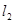 交
交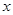 轴于
轴于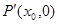 点,
点,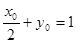 ,
,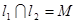 .
.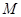 的轨迹
的轨迹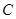 的方程;
的方程;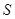 、
、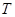 ,已知点
,已知点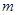 )在线段
)在线段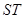 的垂直平分线上且
的垂直平分线上且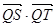 ≤4,求实数
≤4,求实数 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为 .
.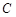 的标准方程;
的标准方程;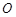 的直线
的直线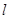 与椭圆
与椭圆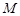 、
、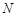 ,且直线
,且直线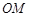 、
、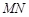 、
、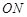 的斜率依次成等比数列,求△
的斜率依次成等比数列,求△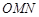 面积的取值范围.
面积的取值范围.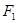 、
、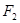 分别为椭圆
分别为椭圆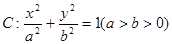 的左、右两个焦点.
的左、右两个焦点.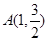 到
到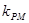 、
、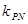 时, 求证:
时, 求证: 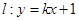 过定点
过定点 ,动点
,动点 满足
满足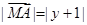 ,动点
,动点 .
.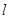 与
与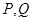 两点,以
两点,以 .
.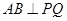 ;②若直线
;②若直线 与
与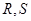 两点,求四边形
两点,求四边形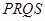 面积的最大值.
面积的最大值. O
O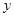 中,直线
中,直线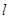 与抛物线
与抛物线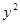 =2
=2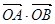 =3”是真命题;
=3”是真命题;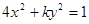 的曲线是焦点在
的曲线是焦点在 上的椭圆 ,求
上的椭圆 ,求 的取值范围
的取值范围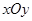 中,以
中,以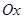 轴为始边作两个锐角
轴为始边作两个锐角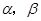 ,它们的终边分别交单位圆于
,它们的终边分别交单位圆于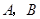 两点.已知
两点.已知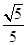 ,
,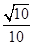 .
.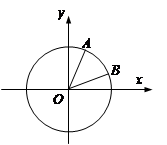
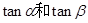 的值;(2)求
的值;(2)求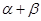 的值.
的值.