题目内容
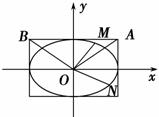
如图,已知椭圆C: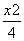 +y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.
(1)设P是椭圆C上任意一点,若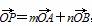 ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
(2)若M、N是椭圆C上两上动点,且直线OM、ON的斜率之积等于直线OA、OB的斜率之积,试探求△OMN的 面积是否为定值,说明理由.
面积是否为定值,说明理由.
(1)证明 易求A(2,1),B(-2,1).(2分)
 所以
所以 +(m+n)2=1,即m2+n2=
+(m+n)2=1,即m2+n2=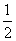 .故点Q(m,n)在定圆x2+y2=
.故点Q(m,n)在定圆x2+y2=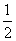 上.(8分)
上.(8分)
(2)解 设M(x1,y1),N(x2,y2),则 =-
=- .
.
平方得x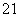 x
x =16y
=16y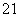 y
y =(4-x
=(4-x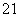 )(4-x
)(4-x ),即x
),即x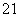 +x
+x =4.(10分)
=4.(10分)
因为直线MN的方程为(x2-x1)x-(y2-y1)y+x1y2-x2y1=0,
所以O到直线MN的距离为
d=
所以△OMN的面积S=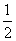 MN·d
MN·d
 =
= =1.
=1.
故△OMN的面积为定值1.(16分)

练习册系列答案
相关题目
在2014年3月15日,某超市对某种商品的销售量及其售价进行调查分析,发现售价x元和销售量y件之间的一组数据如下表所示:
| 售价x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
由散点图可知,销售量y与售价x之间有较好的线性相关关系,其线性回归方程是:
y= -3.2x+a,则a=( )
A. -24 B. 35.6 C. 40.5 D. 40
 有共同的渐近线且过点A(2,-3)求双曲线标准方程
有共同的渐近线且过点A(2,-3)求双曲线标准方程 满足条件
满足条件 (k为常数),若
(k为常数),若 的最大值为8,则k=_________.
的最大值为8,则k=_________. 椭圆C:
椭圆C: (a>b>0)上任一点P到两个焦点的距离的和为2
(a>b>0)上任一点P到两个焦点的距离的和为2 ,P与椭圆长轴两顶点连线的斜率之积为-
,P与椭圆长轴两顶点连线的斜率之积为- .设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).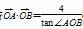 (O为坐标原点),求|y1-y2|的值;
(O为坐标原点),求|y1-y2|的值;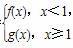 若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.
若P是曲线y=F(x)上异于原点O的任意一点,在曲线y=F(x)上总存在另一点Q,使得△POQ中的∠POQ为钝角,且PQ的中点在y轴上,求a的取值范围.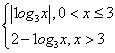 ,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围为( )
,若a,b,c互不相等,且f(a)=f(b)=f(c),则a+b+c的取值范围为( )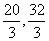 ) B.(
) B.( ) C.(
) C.(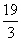 ,12) D.(6,l2)
,12) D.(6,l2) B.
B. C.
C. D.
D.

 的正方形,俯视图
的正方形,俯视图 A.
A. B.
B. 
 D.
D.