题目内容
已知 椭圆C:
椭圆C: (a>b>0)上任一点P到两个焦点的距离的和为2
(a>b>0)上任一点P到两个焦点的距离的和为2 ,P与椭圆长轴两顶点连线的斜率之积为-
,P与椭圆长轴两顶点连线的斜率之积为- .设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
.设直线l过椭圆C的右焦点F,交椭圆C于两点A(x1,y1),B(x2,y2).
(1)若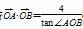 (O为坐标原点),求|y1-y2|的值;
(O为坐标原点),求|y1-y2|的值;
(2)当直线l与两坐标轴都不垂直时,在x轴上是否总存在点Q,使得直线QA,QB的倾斜角互为补角?若存在,求出点Q坐标;若不存在,请说明理由.
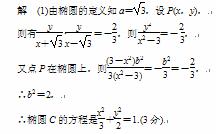
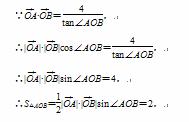 又S△AOB=
又S△AOB=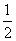 |y1-y2|×1,故|y1-y2|=4.(7分)
|y1-y2|×1,故|y1-y2|=4.(7分)
(2)假设存在一点Q(m,0),使得直线QA,QB的倾斜角互为补角,
依题意可知直线l斜率存在且不为零,
直线l的方程为y=k(x-1)(k≠0),
由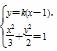 消去y得(3k2+2)x2-6k2x+3k2-6=0,(9分)
消去y得(3k2+2)x2-6k2x+3k2-6=0,(9分)
设A(x1,y1),B(x2,y2),则
∵直线QA,QB的倾斜角互为补角,
∴kQA+kQB=0,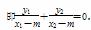
又y1=k(x1-1),y2=k(x2-1),
代入上式可得2x1x2+2m-(m+1)(x1+x2)=0,
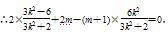 即2m-6=0,∴m=3,
即2m-6=0,∴m=3,
∴存在Q(3,0)使得直线QA,QB的倾斜角互为补角.(16分)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 C.2i D.
C.2i D.
 的图象上一点,等比数列
的图象上一点,等比数列 的首项为c,且前n项和
的首项为c,且前n项和
 和
和 的通项公式;
的通项公式; 的最小正整数n是多少?
的最小正整数n是多少? (a为常数
(a为常数 ).
). x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)
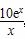 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)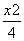 +y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.
+y2=1,A、B是四条直线x=±2,y=±1所围成的两个顶点.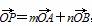 ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程; 面积是否为定值,说明理由.
面积是否为定值,说明理由.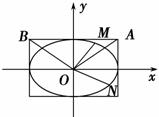
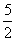 )x,若对任意的x∈[a, a+l],
)x,若对任意的x∈[a, a+l], 为偶函数,且
为偶函数,且 若函数
若函数 ,则
,则 = .
= .