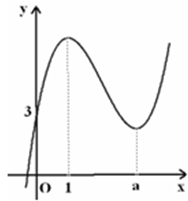
题目内容
已知函数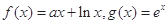 .
.
(I)当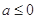 时,求
时,求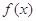 的单调区间
的单调区间
(Ⅱ)若不等式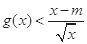 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;
(Ⅲ)定义:对于函数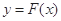 和
和 在其公共定义域内的任意实数
在其公共定义域内的任意实数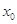 ,称
,称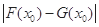 的值为两函数在
的值为两函数在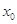 处的差值。证明:当
处的差值。证明:当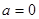 时,函数
时,函数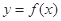 和
和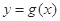 在其公共定义域内的所有差值都大干2。
在其公共定义域内的所有差值都大干2。
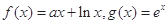 .
.(I)当
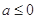 时,求
时,求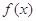 的单调区间
的单调区间(Ⅱ)若不等式
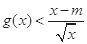 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;(Ⅲ)定义:对于函数
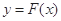 和
和 在其公共定义域内的任意实数
在其公共定义域内的任意实数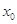 ,称
,称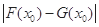 的值为两函数在
的值为两函数在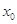 处的差值。证明:当
处的差值。证明:当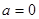 时,函数
时,函数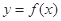 和
和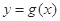 在其公共定义域内的所有差值都大干2。
在其公共定义域内的所有差值都大干2。(I) a=0时,f(x)在(0,+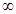 )上单调递增;当a<0时,f(x)在
)上单调递增;当a<0时,f(x)在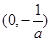 上单调递增;f(x)在
上单调递增;f(x)在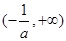 上单调递减.(Ⅱ) m<0.(Ⅲ)证明详见解析.
上单调递减.(Ⅱ) m<0.(Ⅲ)证明详见解析.
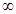 )上单调递增;当a<0时,f(x)在
)上单调递增;当a<0时,f(x)在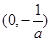 上单调递增;f(x)在
上单调递增;f(x)在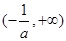 上单调递减.(Ⅱ) m<0.(Ⅲ)证明详见解析.
上单调递减.(Ⅱ) m<0.(Ⅲ)证明详见解析.试题分析:(I)首先求出原函数的导数,然后分类求出
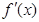 >0或
>0或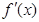 <0的解集,最后根据导数的性质,得出结论即可.(Ⅱ)由已知可知
<0的解集,最后根据导数的性质,得出结论即可.(Ⅱ)由已知可知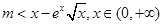 有解,构造函数
有解,构造函数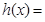
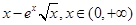 ,求导
,求导 ,利用基本不等式判断导数的符号,确定函数
,利用基本不等式判断导数的符号,确定函数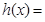
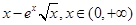 的单调性,求出最大值即可.(Ⅲ) 首先确定公共定义域(0,+
的单调性,求出最大值即可.(Ⅲ) 首先确定公共定义域(0,+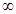 ),
), ,然后构造函数
,然后构造函数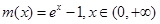 和
和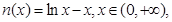 利用导函数的性质求出它们的单调性,极值点和极值,即可确定最值,求得
利用导函数的性质求出它们的单调性,极值点和极值,即可确定最值,求得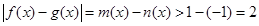 .
.试题解析:(I)f(x)的定义域是(0,+
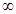 ),
),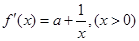 .
.1.当a=0时,
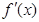 >0,所以f(x)在(0,+
>0,所以f(x)在(0,+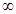 )上单调递增;
)上单调递增;2.当a<0时,由
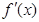 =0,解得
=0,解得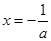 ,则
,则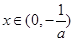 时,
时,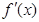 >0,所以f(x)在
>0,所以f(x)在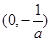 上单调递增;
上单调递增;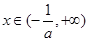 时,
时,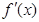 <0,所以f(x)在
<0,所以f(x)在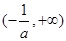 上单调递减.
上单调递减.综上所述,a=0时,f(x)在(0,+
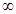 )上单调递增;当a<0时,f(x)在
)上单调递增;当a<0时,f(x)在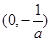 上单调递增;f(x)在
上单调递增;f(x)在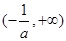 上单调递减.
上单调递减.(Ⅱ) 由题意
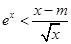 有解,即
有解,即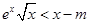 有解,
有解,因此只需
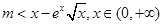 有解即可.
有解即可.设
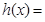
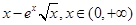 ,则
,则
因为
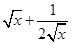
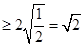 ,且
,且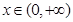 时,
时,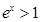 .
.所以
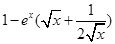 <0,即
<0,即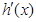 <0,
<0,故h(x)在
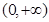 单调递减,
单调递减,所以h(x)<h(0)=0,故m<0.
(Ⅲ)当a=0时,
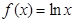 ,f(x)与g(x)的公共定义域为
,f(x)与g(x)的公共定义域为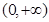 ,
,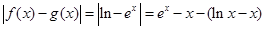 ,
,设
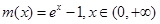 ,则
,则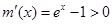 ,
,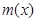 在
在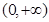 上单调递增,所以
上单调递增,所以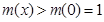 .
.又设
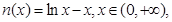 则
则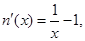
当
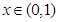 时,
时, ,
,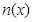 单调递增;
单调递增;当
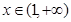 时,
时,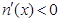 ,
,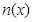 单调递减;
单调递减;所以x=1为函数
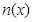 的极大值点,即
的极大值点,即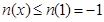 ,故
,故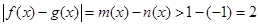 .
.即公共定义域内任一点差值都大于2.

练习册系列答案
相关题目
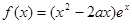 ,其中
,其中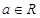 ,曲线
,曲线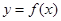 在点
在点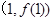 处的切线垂直于
处的切线垂直于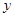 轴.
轴.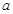 的值;
的值;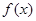 的极值.
的极值.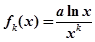 为
为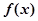 的
的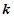 阶函数.
阶函数.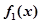 的单调区间;
的单调区间;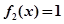 的解的个数;
的解的个数;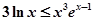 .
.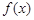 的导函数是
的导函数是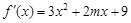 ,
,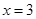 处取得极值,且
处取得极值,且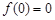 .
.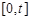 上的最大值为
上的最大值为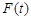 ,若对任意的
,若对任意的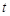
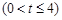 总有
总有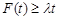 成立,求
成立,求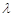 的取值范围;
的取值范围;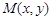 是曲线
是曲线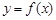 上的任意一点.当
上的任意一点.当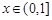 时,求直线OM斜率的最小值,据此判断
时,求直线OM斜率的最小值,据此判断 的大小关系,并说明理由.
的大小关系,并说明理由.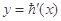 的图象如图,f(x)=6lnx+h(x)
的图象如图,f(x)=6lnx+h(x)
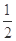 )上是单调函数,求实数m的取值范围;
)上是单调函数,求实数m的取值范围;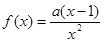 ,其中
,其中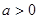 .
.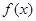 的单调区间;
的单调区间;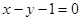 是曲线
是曲线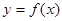 的切线,求实数
的切线,求实数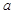 的值;
的值;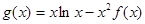 ,求
,求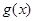 在区间
在区间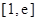 上的最小值.(
上的最小值.(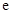 为自然对数的底数)
为自然对数的底数)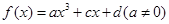 是R上的奇函数,当
是R上的奇函数,当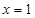 时
时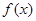 取得极值
取得极值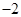 .
.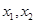
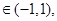 不等式
不等式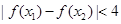 恒成立.
恒成立.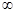 ,
,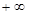 )内有定义,对于给定的正数k,定义函数:
)内有定义,对于给定的正数k,定义函数: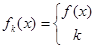
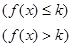 ,取函数
,取函数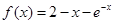 ,若对任意的x∈(-
,若对任意的x∈(-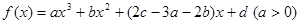 的图像如图所示,且
的图像如图所示,且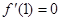 .则
.则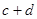 的值是 .
的值是 .