��Ŀ����
(��������18��) �����3��С�⣬��1С������4�֣���2С������6��. ��3С������8��.
���ģ��������� ������ѡȡ��������ı�������ԭ�������е��Ⱥ���õ������г�Ϊ��ԭ�����е�һ��������. ijͬѧ��ѧϰ����һ������֮�����о�����Ϊ
������ѡȡ��������ı�������ԭ�������е��Ⱥ���õ������г�Ϊ��ԭ�����е�һ��������. ijͬѧ��ѧϰ����һ������֮�����о�����Ϊ ,����Ϊ
,����Ϊ ������Ȳ�����
������Ȳ�����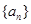 �����������⣬Ϊ�ˣ���ȡ�����е�һ��
�����������⣬Ϊ�ˣ���ȡ�����е�һ�� ��������
�������� �͵�����
�͵����� .
.
(1) �� �ɵȱ�����,��
�ɵȱ�����,�� ��ֵ��
��ֵ��
(2) �� ,
,  ������Ȳ�����
������Ȳ�����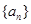 �У��Ƿ��������������
�У��Ƿ�������������� ��ʹ������
��ʹ������ Ϊ�ȱ����У������ڣ����������
Ϊ�ȱ����У������ڣ���������� ��ͨ�ʽ��֤�����������ڣ�˵�����ɣ�
��ͨ�ʽ��֤�����������ڣ�˵�����ɣ�
(3) �����о������в�����һ�����⣺����������Ϊ������ ������Ϊ������
������������ (
( )������ȱ��� ��
)������ȱ��� �� ,�ܿ����ҵ�һ��������
,�ܿ����ҵ�һ�������� ,ʹ��
,ʹ�� ���ɵȲ����С�. ���ǣ���������
���ɵȲ����С�. ���ǣ��������� ����ȡ����
����ȡ���� ����
���� ��
�� �Ĵ�С��ϵȥ�жϸ������Ƿ���ȷ. �����õ�ʲô���ۣ�
�Ĵ�С��ϵȥ�жϸ������Ƿ���ȷ. �����õ�ʲô���ۣ�
��1��d=0��2������bn=4n-1Ϊ����������һ�������У���Ϊbn="1+3M" ="1+3"
[(M+1)-1]��{an}�еĵ�M+1�3��ͨ��������Եõ� >
> ���Ӷ�ԭ����Ϊ������
���Ӷ�ԭ����Ϊ������
��������
���������(1)��a32=a1a5�� ����2��
��(a1+2d)2=a1(a1+4d)����d=0. ����4��
(2) an=1+3(n-1)����bn=4n-1��Ϊ����������һ��������. ����7��
��Ϊbn=4n-1=(1+3)n-1=1+ 3+
3+ 32+��+
32+��+ 3n-1=1+3M, ����9��
3n-1=1+3M, ����9��
����M= +
+ 3+��+
3+��+ 3n-2��������
3n-2��������
����,bn="1+3M" ="1+3" [(M+1)-1]��{an}�еĵ�M+1���֤. ����11��
(ע��bn��ͨ�ʽ��Ψһ)
(3) ������������. ����12��
����֪�ɵ� ,
,
���, ,��
,�� ,
,
��  , ����15��
, ����15��
���� ������������
������������ ����
���� ,
,
�� ������
������ ������������
������������ ,
,
 ,
,
���ԣ� >
> ,�Ӷ�ԭ����Ϊ������.
����18��
,�Ӷ�ԭ����Ϊ������.
����18��
���㣺��С����Ҫ����Ȳ����к͵ȱ��������ۺ����㣬����ѧ���������⡢����������������������Լ�������֤������.
�������Ȳ����к͵ȱ������Ǹ߿��г����������������У����ǵ��ж���ͨ�ʽ��ǰn���ʽ��Ӧ��Ҫ�������գ����Ӧ��.

 ������
������ ���Ҷ������������n����
���Ҷ������������n����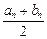 ��0ʱ, ��[
��0ʱ, ��[ ,
,  ]=
]= ,
, 
 ]��
]�� }�ǵȱ����У�
}�ǵȱ����У� ����֤
����֤
 ��
�� ��ʹ������
��ʹ������ Ϊ�������У���˵������
Ϊ�������У���˵������ �����ߵľ������5��
�����ߵľ������5�� ����A��C��D��B�ĵ�,��֤��
����A��C��D��B�ĵ�,��֤�� Ϊ��ֵ;
Ϊ��ֵ; ��
�� ��
�� ���֮�͵���Сֵ��
���֮�͵���Сֵ��
 ����������Ϊ
����������Ϊ ����������
���������� ����
���� Ϊ
Ϊ �����ֵ��������
�����ֵ�������� Ϊ
Ϊ 3��5��4��7�Ĵ�������Ϊ3��5��5��7��
3��5��4��7�Ĵ�������Ϊ3��5��5��7�� ���������У���ÿ�����ж���Ϊһ����������
���������У���ÿ�����ж���Ϊһ���������� ��
�� ��д����������Ϊ3��4��4��4����������
��д����������Ϊ3��4��4��4���������� ������Ϊ1��ǰ
������Ϊ1��ǰ ���Ϊ
���Ϊ ��������
�������� ��
�� ������
������ ����
���� .
.  ʱ���ԱȽ�
ʱ���ԱȽ� ��
�� �Ĵ�С����˵�����ɣ�
�Ĵ�С����˵�����ɣ�
 �Ƿ����ǡΪֱ��
�Ƿ����ǡΪֱ��
 �ķ�����������˵���������.
�ķ�����������˵���������.