题目内容
(本题满分18分,第(1)小题6分,第(2)小题6分,第(3)小题6分)
若数列![]() 满足:
满足:![]() 是常数),则称数列
是常数),则称数列![]() 为二阶线性递推数列,且定义方程
为二阶线性递推数列,且定义方程![]() 为数列
为数列![]() 的特征方程,方程的根称为特征根; 数列
的特征方程,方程的根称为特征根; 数列![]() 的通项公式
的通项公式![]() 均可用特征根求得:
均可用特征根求得:
①若方程![]() 有两相异实根
有两相异实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
②若方程![]() 有两相同实根
有两相同实根![]() ,则数列通项可以写成
,则数列通项可以写成![]() ,(其中
,(其中![]() 是待定常数);
是待定常数);
再利用![]() 可求得
可求得![]() ,进而求得
,进而求得![]() .
.
根据上述结论求下列问题:
(1)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(2)当![]() ,
,![]() (
(![]() )时,求数列
)时,求数列![]() 的通项公式;
的通项公式;
(3)当![]() ,
,![]() (
(![]() )时,记
)时,记![]() ,若
,若![]() 能被数
能被数![]() 整除,求所有满足条件的正整数
整除,求所有满足条件的正整数![]() 的取值集合.
的取值集合.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]() (Ⅲ)
(Ⅲ)![]()
解析:
(1)由![]() 可知特征方程为:
可知特征方程为:
![]() ,
, ![]() …………………3分
…………………3分
所以 设 ![]() ,由
,由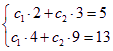 得到
得到![]() ,
,
所以 ![]() ; …………………6分
; …………………6分
(2)由![]() 可以得到
可以得到![]()
设![]() ,则上述等式可以化为:
,则上述等式可以化为:![]() …………………8分
…………………8分
![]() ,所以
,所以![]() 对应的特征方程为:
对应的特征方程为:
![]() ,
,![]() …………………10分
…………………10分
所以令 ![]() ,由
,由![]() 可以得出
可以得出
所以![]() …………………11分
…………………11分
即 ![]() …………………12分
…………………12分
(3)同样可以得到通项公式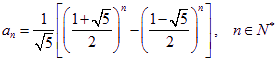 ………14分
………14分
所以![]()
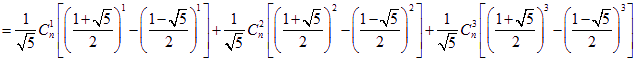

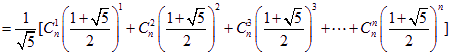
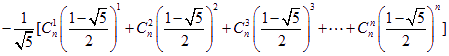

即 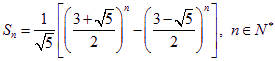 …………………14分
…………………14分
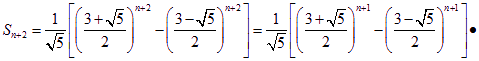

![]()
即 ![]() ,
,![]() …………………16分
…………………16分
因此![]() 除以
除以![]() 的余数,完全由
的余数,完全由![]() 除以
除以![]() 的余数确定,
的余数确定,
因为![]()
![]() 所以
所以 ![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
由以上计算及![]() 可知,数列
可知,数列![]() 各项除以
各项除以![]() 的余数依次是:
的余数依次是:
![]() 它是一个以
它是一个以![]() 为周期的数列,从而
为周期的数列,从而![]() 除以
除以![]() 的余数等价于
的余数等价于![]() 除以
除以![]() 的余数,所以
的余数,所以![]() ,
,![]() ,
,
即所求集合为:![]() …………………18分
…………………18分

练习册系列答案
相关题目
 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当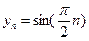 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
( 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
. ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
( ,
,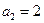 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
(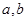 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
.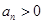 ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
(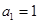 ,
,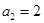 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,其中
,其中 .
. 时,设
时,设 ,
, ,求
,求 的解析式及定义域;
的解析式及定义域; 时,求
时,求 的最小值;
的最小值; ,当
,当 时,
时, 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围. 是等差数列,且公差为
是等差数列,且公差为 ,若数列
,若数列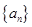 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”. ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”; 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么? 是数列
是数列 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使 ;若存在,求
;若存在,求