题目内容
已知向量a=（1，sinx+
cosx），b=（1，y），若a∥b且有函数y=f（x）．
（I）若x∈[-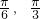
]，求函数y=f（x）的值域；
（II）已知锐角△ABC的三内角分别是A、B、C，若有f（A-
，求边AC的长．
解：（I）由
，得y=sinx+cosx=2sin（x+
）
∵x∈[-
，]
∴x+∈[，
]
∴sin（x+）∈[
，1]
∴函数的值域为[1，2]
（Ⅱ）由f（A-=，得2sinA=
∵△ABC为锐角三角形，则A=
由正弦定理得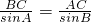
及BC=
∴sinB=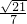
∴AC=2
分析：（I）根据，得出y=2sin（x+），然后根据x的取值范围求得x+∈[，]，进而得出值域；
（Ⅱ）首先求出2sinA=，根据△ABC为锐角三角形求出∠A的度数，然后由正弦定理得出sinB=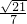
，即可求出结果
点评：本题主要考查正弦定理，平面向量共线（平行）的坐标表示，解题过程中要注意角的范围和三角形的形状，属于中档题．
，得y=sinx+cosx=2sin（x+）∵x∈[-
，]∴x+
∈[，]∴sin（x+
）∈[，1]∴函数的值域为[1，2]
（Ⅱ）由f（A-
=，得2sinA=∵△ABC为锐角三角形，则A=
由正弦定理得
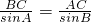及BC=∴sinB=
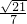
∴AC=2
分析：（I）根据
，得出y=2sin（x+），然后根据x的取值范围求得x+∈[，]，进而得出值域；（Ⅱ）首先求出2sinA=
，根据△ABC为锐角三角形求出∠A的度数，然后由正弦定理得出sinB=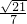，即可求出结果
点评：本题主要考查正弦定理，平面向量共线（平行）的坐标表示，解题过程中要注意角的范围和三角形的形状，属于中档题．
练习册系列答案
相关题目