题目内容
 .
.
(1)确定函数f(x)的解析式;
(2)当x∈(-1,1)时判断函数f(x)的单调性,并证明;
(3)解不等式f(2x-1)+f(x)<0.
解:(1)由题意可知f(-x)=-f(x)
∴ =-
=-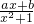
∴-ax+b=-ax-b,∴b=0
∵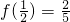 ,∴a=1
,∴a=1
∴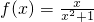 ;
;
(2)当x∈(-1,1)时,函数f(x)单调增,证明如下:
∵ ,x∈(-1,1)
,x∈(-1,1)
∴f′(x)>0,∴当x∈(-1,1)时,函数f(x)单调增;
(3)∵f(2x-1)+f(x)<0,且f(x)为奇函数
∴f(2x-1)<f(-x)
∵当x∈(-1,1)时,函数f(x)单调增,
∴
∴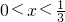
∴不等式的解集为(0, ).
).
分析:(1)利用函数为奇函数,可得b=0,利用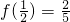 ,可得a=1,从而可得函数f(x)的解析式;
,可得a=1,从而可得函数f(x)的解析式;
(2)利用导数的正负,可得函数的单调性;
(3)利用函数单调增,函数为奇函数,可得具体不等式,从而可解不等式.
点评:本题主要考查应用奇偶性来求函数解析式,考查函数的单调性,还考查了综合运用奇偶性和单调性来解不等式的能力,属于中档题.
∴
 =-
=-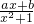
∴-ax+b=-ax-b,∴b=0
∵
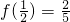 ,∴a=1
,∴a=1∴
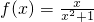 ;
;(2)当x∈(-1,1)时,函数f(x)单调增,证明如下:
∵
 ,x∈(-1,1)
,x∈(-1,1)∴f′(x)>0,∴当x∈(-1,1)时,函数f(x)单调增;
(3)∵f(2x-1)+f(x)<0,且f(x)为奇函数
∴f(2x-1)<f(-x)
∵当x∈(-1,1)时,函数f(x)单调增,
∴

∴
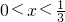
∴不等式的解集为(0,
 ).
).分析:(1)利用函数为奇函数,可得b=0,利用
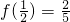 ,可得a=1,从而可得函数f(x)的解析式;
,可得a=1,从而可得函数f(x)的解析式;(2)利用导数的正负,可得函数的单调性;
(3)利用函数单调增,函数为奇函数,可得具体不等式,从而可解不等式.
点评:本题主要考查应用奇偶性来求函数解析式,考查函数的单调性,还考查了综合运用奇偶性和单调性来解不等式的能力,属于中档题.

练习册系列答案
相关题目