题目内容
14．计算${（{\frac{1+i}{1-i}}）^{2017}}$=（ ）| A． | -1 | B． | i | C． | -i | D． | 1 |
分析 直接利用复数代数形式的乘除运算化简，再由虚数单位i的运算性质求值．
解答 解：${（{\frac{1+i}{1-i}}）^{2017}}$=$[\frac{（1+i）^{2}}{（1-i）（1+i）}]^{2017}=（\frac{2i}{2}）^{2017}={i}^{2017}=i$．
故选：B．
点评 本题考查复数代数形式的乘除运算，考查计算能力，是基础题．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
5．设x0为函数f（x）=sinπx的零点，且满足$|{x_0}|+f（{x_0}+\frac{1}{2}）＜11$，则这样的零点有（ ）
| A． | 18个 | B． | 19个 | C． | 20个 | D． | 21个 |
2．已知点p（x，y）满足$\left\{\begin{array}{l}x+y-2\sqrt{2}≥0\\ x≤2\sqrt{2}\\ y≤2\sqrt{2}\end{array}\right.$过点p（x，y）向圆x2+y2=1做两条切线，切点分别是点A和点B，则当∠APB最大时，$\overrightarrow{PA}•\overrightarrow{PB}$的值是（ ）
| A． | 2 | B． | 3 | C． | $\frac{5}{2}$ | D． | $\frac{3}{2}$ |
9．已知函数$f（x）=sin（{ωx+φ}）+1（{ω＞0，0≤φ≤\frac{π}{2}}）$的图象的相邻两对称轴之间的距离为π，且在$x=\frac{π}{6}$时取得最大值2，若$f（α）=\frac{9}{5}$，且$\frac{π}{6}＜α＜\frac{2π}{3}$，则$sin（{2α+\frac{2π}{3}}）$的值为（ ）
| A． | $\frac{12}{25}$ | B． | $-\frac{12}{25}$ | C． | $\frac{24}{25}$ | D． | $-\frac{24}{25}$ |
19．设f'（x）是函数f（x）定义在（0，+∞）上的导函数，满足$xf'（x）+2f（x）=\frac{1}{x^2}$，则下列不等式一定成立的是（ ）
| A． | $\frac{f（e）}{e^2}＞\frac{{f（{e^2}）}}{e}$ | B． | $\frac{f（2）}{9}＜\frac{f（3）}{4}$ | C． | $\frac{f（2）}{e^2}＞\frac{f（e）}{4}$ | D． | $\frac{f（e）}{e^2}＜\frac{f（3）}{9}$ |
6．
某几何体的三视图如图所示，则这个几何体的体积为（ ）
某几何体的三视图如图所示，则这个几何体的体积为（ ）| A． | 4 | B． | 8 | C． | $\frac{20}{3}$ | D． | $\frac{26}{3}$ |
17．某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在[50，100]内，发布成绩使用等级制各等级划分标准见下表，规定：A、B、C三级为合格等级，D为不合格等级．
为了解该校高一年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图如图1所示，样本中分数在80分及以上的所有数据的茎叶图如图2所示．
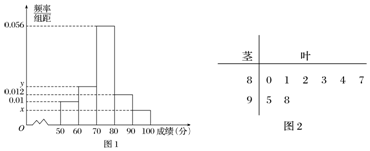
（1）求n和频率分布直方图中x，y的值；
（2）根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生中任选3人，求至少有1人成绩是合格等级的概率．
| 百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
（1）求n和频率分布直方图中x，y的值；
（2）根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生中任选3人，求至少有1人成绩是合格等级的概率．