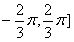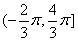题目内容

设函数f（x）=xtanx，若x1，x2∈[-
π
2
，
π
2
]且f（x1）＞f（x2），则下列结论中必成立的是（　　）
A．x1＞x2B．x12＜x22C．x12＞x22D．x1＜x2
容易判断，函数为偶函数，由f（x1）＞f（x2），得f（|x1|）＞f（|x2|），
y′=（xtanx）′=tanx+xsec2x；当x＞0时，y′＞0，函数为增函数，所以|x1|＞|x2|，所以 x12＞x22

故选C．
练习册系列答案
相关题目
已知m=（cosx，2sinx），n=（2cosx，-sinx），f（x）=m·n。
（1）求f（-π）的值；
（2）当x∈[0，]时，求g（x）=f（x）+sin2x的最大值和最小值。
函数f(x)=tan(x+
π
4
)的单调增区间为（　　）
A．(kπ-
π
2
，kπ+
π
2
)，k∈Z		B．（kπ，（k+1）π），k∈Z
C．(kπ-
3π
4
，kπ+
π
4
)，k∈Z		D．(kπ-
π
4
，kπ+
3π
4
)，k∈Z
下列不等式中，正确的是（　　）
A．sin220°＜sin240°B．cos
15π
7
＜cos
13π
6
C．tan(-
13π
4
)＜tan(-
17π
5
)		D．sin174°＞cos160°
函数f（x）=
1-cos2x
cosx
（　　）
A．在[0，
π
2
），（
π
2
，π]上递增，在[π，
3π
2
），（
3π
2
，2π]上递减
B．在[0，
π
2
），[π，
3π
2
）上递增，在（
π
2
，π]，（
3π
2
，2π]上递减
C．在（
π
2
，π]，（
3π
2
，2π]上递增，在[0，
π
2
），[π，
3π
2
）上递减
D．在[π，
3π
2
），（
3π
2
，2π]上递增，在[0，
π
2
），（
π
2
，π]上递减
函数y=tan（
π
2
x+
π
3
）的周期为______单调区间为______．
满足tanx＜0的x值范围是（　　）
A．{x|-
π
2
+kπ＜x＜kπ，k∈Z}		B．{x|-
π
2
+2kπ＜x＜2kπ，k∈Z}
C．{x|kπ＜x＜
π
2
+kπ，k∈Z}		D．{x|2kπ＜x＜
π
2
+2kπ，k∈Z}
若在区间的最小值为，则a的取值范围是（    ）。
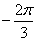函数y=sin2x+2cosx在区间[，a]上的最小值为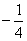，则a的取值为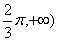

[     ]

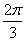A．[
B．[0，]
C．（
D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网