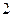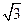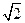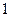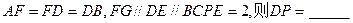题目内容
如图,在等腰梯形ABCD中,AB∥CD,且AB=2CD,设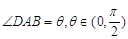 ,以A,B为焦点且过点D的双曲线离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则( )
,以A,B为焦点且过点D的双曲线离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则( )
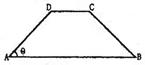
 ,以A,B为焦点且过点D的双曲线离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则( )
,以A,B为焦点且过点D的双曲线离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则( )A.随着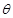 角增大,e1增大,e1 e2为定值 角增大,e1增大,e1 e2为定值 | B.随着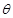 角增大,e1减小,e1 e2为定值 角增大,e1减小,e1 e2为定值 |
C.随着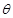 角增大,e1增大,e1 e2也增大 角增大,e1增大,e1 e2也增大 | D.随着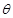 角增大,e1减小,e1 e2也减小 角增大,e1减小,e1 e2也减小 |

B
设CD=2 AB=4
以A,B为焦点且过点D的双曲线 2c=AB=4 c=2
AD= ,BD=
,BD=  ,2a="DB-DA="
,2a="DB-DA=" 
e1= , 随着
, 随着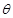 角增大,BD的值在增大,AD的值在减少,所以2a在增大,2c不变,所以利息率在减小。
角增大,BD的值在增大,AD的值在减少,所以2a在增大,2c不变,所以利息率在减小。
以C,,D为焦点且过点A的椭圆
2c=2 c=1
2a=AD+AC AC=BD
2a= e2=
e2= ,
,
e1 e2= ,
,
随着θ角增大 e1减小,e1 e2不变
以A,B为焦点且过点D的双曲线 2c=AB=4 c=2
AD=
 ,BD=
,BD=  ,2a="DB-DA="
,2a="DB-DA=" 
e1=
 , 随着
, 随着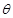 角增大,BD的值在增大,AD的值在减少,所以2a在增大,2c不变,所以利息率在减小。
角增大,BD的值在增大,AD的值在减少,所以2a在增大,2c不变,所以利息率在减小。 以C,,D为焦点且过点A的椭圆
2c=2 c=1
2a=AD+AC AC=BD
2a=
 e2=
e2= ,
, e1 e2=
 ,
,随着θ角增大 e1减小,e1 e2不变

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
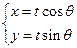 与圆
与圆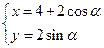 相切,则
相切,则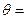 _______________。
_______________。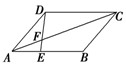





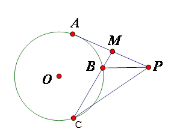
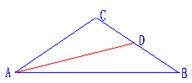
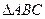 中,
中, 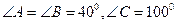 ,
,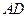 平分
平分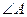 交
交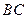 于点
于点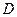 .
.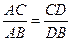
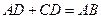
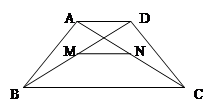
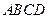 中,
中,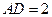 ,
,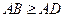 ,
,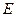 为
为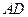 的中点,
的中点,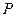 是
是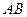 边上一动点.
边上一动点.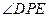 取得最大时,
取得最大时,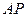 等于
等于