题目内容
在 中,
中, 分别是角A、B、C的对边,且满足:
分别是角A、B、C的对边,且满足: .
.
(I)求角C;
(II)求函数 的单调减区间和取值范围.
的单调减区间和取值范围.
(1) (2) 单调减区间是
(2) 单调减区间是 ,取值范围是
,取值范围是 .
.
解析试题分析:解(I)由已知 可得:
可得: ,在三角形ABC中,由正弦定理可得:
,在三角形ABC中,由正弦定理可得: ,即
,即
= ,所以
,所以 ,又因为
,又因为 ,所以
,所以 ,在三角形ABC中,故
,在三角形ABC中,故
(II) =
= ,在
,在 中,
中, ,所以y=
,所以y=
 ,因为
,因为 ,所以
,所以 ,故函数
,故函数 在
在
 上单调递增,且在区间
上单调递增,且在区间 上
上 的取值范围是
的取值范围是 ,所以
,所以
 的单调减区间是
的单调减区间是 ,值域是
,值域是 .
.
考点:正弦定理,三角恒等变换
点评:解决的关键是利用正弦定理得到边角化简,然后结合恒等变换来得到单一三角函数,进而求解其性质,属于基础题。

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目

 ,向量
,向量
 ,且满足
,且满足 。
。 ,求角
,求角 ;
; ,△ABC的面积
,△ABC的面积 ,求△ABC的周长。
,求△ABC的周长。 中,
中,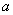 、
、 、
、 分别为角
分别为角 、
、 、
、 所对的边,且
所对的边,且
 ,且△
,且△ ,求
,求 的值.
的值. ,解三角形ABC。
,解三角形ABC。 中内角
中内角 的对边分别为
的对边分别为 ,向量
,向量 ,且
,且
 的大小,
的大小, ,求
,求 的最大值
的最大值 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
. 的大小;(2)若
的大小;(2)若 ,求
,求 的取值范围.
的取值范围.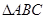 中,内角A、B、C的对边分别是
中,内角A、B、C的对边分别是 、b、c,已知
、b、c,已知 ,且
,且 的夹角为
的夹角为 。
。 ,三角形的面积
,三角形的面积 ,求
,求 的值。
的值。 ,
,
 ,且
,且 ∥
∥ ,
, ,且△ABC的面积小于
,且△ABC的面积小于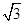 ,求角B的取值范围.
,求角B的取值范围.