题目内容
(本小题满分12分)设锐角△ABC的三内角A,B,C的对边分别为 A,b,c,已知向量 ,
,
 ,且
,且 ∥
∥ .
.
(1) 求角A的大小;
(2) 若 ,
, ,且△ABC的面积小于
,且△ABC的面积小于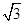 ,求角B的取值范围.
,求角B的取值范围.
(1) ;(2)
;(2) 。
。
解析试题分析:(1)因为 ∥
∥ ,则
,则 ,即
,即 .
.
所以 ,即
,即 ,即
,即 .
.
A是锐角,则 ,所以
,所以 .
.
(2)因为 ,
, ,则
,则



 .
.
由已知, ,即
,即 .
.
因为B是锐角,所以 ,即
,即 ,故角B的取值范围是
,故角B的取值范围是 .
.
考点:平面向量平行的条件;二倍角公式;三角形的面积公式。
点评:三角函数和其他知识点相结合往往是第一道大题,一般较为简单,应该是必得分的题目。而有些同学在学习中认为这类题简单,自己一定会,从而忽略了对它的练习,因此导致考试时不能得满分,甚至不能得分。比如此题在第二问中,就较易忘掉应用第一问求出 的范围。因此我们在平常训练的时候就要要求自己“会而对,对而全”。
的范围。因此我们在平常训练的时候就要要求自己“会而对,对而全”。

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 中,
中, 分别是角A、B、C的对边,且满足:
分别是角A、B、C的对边,且满足: .
. 的单调减区间和取值范围.
的单调减区间和取值范围. ,
, 中,
中, 求
求 的值
的值
 中,
中,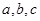 分别是内角
分别是内角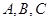 所对的边,且
所对的边,且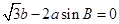 .
. 的大小;
的大小;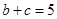 ,且
,且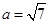 ,求
,求 =(
=( ),
),  =
= ,f(x)=
,f(x)=
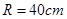 ,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为
,同侧前后两轮胎之间的距离(指轮胎中心之间距离)为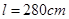 (假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路
(假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路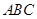 (如图(1)所示,其中
(如图(1)所示,其中 (
( )),且前轮
)),且前轮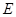 已在
已在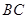 段上时,后轮中心在
段上时,后轮中心在 位置;若前轮中心到达
位置;若前轮中心到达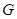 处时,后轮中心在
处时,后轮中心在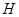 处(假定该汽车能顺利驶上该上坡路). 设前轮中心在
处(假定该汽车能顺利驶上该上坡路). 设前轮中心在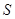 和
和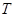 ,且
,且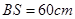 ,
,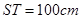 . (其它因素忽略不计)
. (其它因素忽略不计)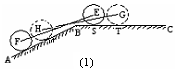
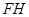 和
和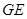 的延长线交于点
的延长线交于点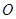 ,
, (cm);
(cm);
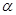 =
=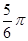 时,后轮中心从
时,后轮中心从 、
、 、
、 ,且
,且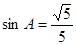 ,
,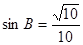 。
。 -1,求
-1,求