题目内容
已知直线l:kx-y+1+2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线l不经过第四象限,求k的取值范围;
(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.
解 (1)证明:方法一:直线l的方程可化为y=k(x+2)+1,
故无论k取何值,直线l总过定点(-2,1).
方法二:设直线l过定点(x0,y0),则kx0-y0+1+2k=0对任意k∈R恒成立,即(x0+2)k-y0+1=0恒成立,∴x0+2=0,-y0+1=0,
解得x0=-2,y0=1,故直线l总过定点(-2,1).
(2)直线l的方程为y=kx+2k+1,
则直线l在y轴上的截距为2k+1,

 当且仅当4k=
当且仅当4k= ,即k=
,即k= 时,取等号.
时,取等号.
故S的最小值为4,此时直线l的方程为x-2y+4=0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 +
+ <
<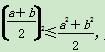 ,则p是q成立的( )
,则p是q成立的( )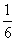 .
. ,
,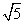 -
-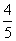 π B.
π B.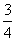 π
π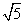 )π D.
)π D. π
π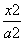 -
-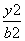 =1(a>0,b>0)的右焦点为F,O为坐标原点.若以F为圆心,FO为半径的圆与双曲线C的渐近线y=
=1(a>0,b>0)的右焦点为F,O为坐标原点.若以F为圆心,FO为半径的圆与双曲线C的渐近线y= x交于点A(不同于O点),则△OAF的面积为________.
x交于点A(不同于O点),则△OAF的面积为________.