题目内容
求中心在原点,对称轴为坐标轴,且满足下列条件的双曲线方程:(1)经过两点(2
| 7 |
| 2 |
(2)双曲线过点(3,9
| 2 |
| ||
| 3 |
分析:(1)由于不清楚双曲线的焦点在哪条坐标轴上,可设其方程为
-
=1(mn<0),然后把点的坐标分别代入该方程形成方程组,最后解方程组即可.
(2)分别设出焦点在x轴、y轴上的双曲线的方程,然后根据其过定点(3,9
)、离心率e=
=
、且有c2=a2+b2,则列方程组,分别解之即可.
| x2 |
| m |
| y2 |
| n |
(2)分别设出焦点在x轴、y轴上的双曲线的方程,然后根据其过定点(3,9
| 2 |
| c |
| a |
| ||
| 3 |
解答:解:(1)设双曲线方程为
-
=1,
则
,解得m=25,n=75,
∴该双曲线的方程为
-
=1.
(2)若双曲线焦点在x轴上,设其方程为
-
=1,
则
,解得b2=-161(舍去);
若双曲线焦点在y轴上,设其方程为
-
=1,
则
,解得a2=81,b2=9,
所以双曲线的方程为
-
=1.
故双曲线的方程为
-
=1.
| x2 |
| m |
| y2 |
| n |
则
|
∴该双曲线的方程为
| x2 |
| 25 |
| y2 |
| 75 |
(2)若双曲线焦点在x轴上,设其方程为
| x2 |
| a2 |
| y2 |
| b2 |
则
|
若双曲线焦点在y轴上,设其方程为
| y2 |
| a2 |
| x2 |
| b2 |
则
|
所以双曲线的方程为
| y2 |
| 81 |
| x2 |
| 9 |
故双曲线的方程为
| y2 |
| 81 |
| x2 |
| 9 |
点评:本题主要考查双曲线的标准方程与性质,同时考查解方程组的运算能力.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
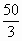 ;
; .
. ,一条渐近线是
,一条渐近线是 的双曲线方程及离心率.
的双曲线方程及离心率. ),(
),( );
); ),离心率
),离心率 .
.