题目内容
【题目】选修4-4:坐标系与参数方程
已知圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).若直线
为参数).若直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(Ⅰ)写出圆![]() 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;
(Ⅱ)若弦长![]() ,求直线
,求直线![]() 的斜率.
的斜率.
【答案】(I)![]() ;(II)
;(II)![]() 或
或![]() .
.
【解析】
试题分析:(I)化极坐标方程为直角坐标方程主要是利用公式![]() ,
,![]() ,
,![]() 来完成.代入可得
来完成.代入可得![]() ,配方得
,配方得![]() ,所以圆心为
,所以圆心为![]() ,半径为
,半径为![]() ;(II)在极坐标方程与参数方程的条件下求解直线与圆的位置关系问题,通常将极坐标方程与参数方程均化为直角坐标方程来解决.由直线
;(II)在极坐标方程与参数方程的条件下求解直线与圆的位置关系问题,通常将极坐标方程与参数方程均化为直角坐标方程来解决.由直线![]() 的参数方程知直线过定点
的参数方程知直线过定点![]() ,直线
,直线![]() 的方程为
的方程为![]() .利用弦长等于
.利用弦长等于![]() 可求得斜率
可求得斜率![]() 或
或![]() .
.
试题解析:(Ⅰ)由![]() ,得
,得![]()
将![]() ,代入可得
,代入可得![]() ,
,
配方,得![]() ,所以圆心为
,所以圆心为![]() ,半径为
,半径为![]() .
.
(Ⅱ)由直线![]() 的参数方程知直线过定点
的参数方程知直线过定点![]() ,
,
则由题意,知直线![]() 的斜率一定存在,因此不妨设直线
的斜率一定存在,因此不妨设直线![]() 的方程为
的方程为![]() 的方程为
的方程为![]() .
.
因为![]() ,所以
,所以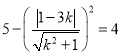 ,解得
,解得![]() 或
或![]()

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】已知函数![]() 的图像两相邻对称轴之间的距离是
的图像两相邻对称轴之间的距离是![]() ,若将
,若将![]() 的图像先向右平移
的图像先向右平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位,所得函数
个单位,所得函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的对称轴及单调区间;
的对称轴及单调区间;
(3)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【题目】现有甲、乙两个投资项目,对甲项目投资十万元,据对市场![]() 份样本数据统计,年利润分布如下表:
份样本数据统计,年利润分布如下表:
年利润 |
|
|
|
频数 |
|
|
|
对乙项目投资十万元,年利润与产品质量抽查的合格次数有关,在每次抽查中,产品合格的概率均为![]() ,在一年之内要进行
,在一年之内要进行![]() 次独立的抽查,在这
次独立的抽查,在这![]() 次抽查中产品合格的次数与对应的利润如下表:
次抽查中产品合格的次数与对应的利润如下表:
合格次数 |
|
|
|
年利润 |
|
|
|
记随机变量![]() 分别表示对甲、乙两个项目各投资十万元的年利润.
分别表示对甲、乙两个项目各投资十万元的年利润.
(1)求![]() 的概率;
的概率;
(2)某商人打算对甲或乙项目投资十万元,判断哪个项目更具有投资价值,并说明理由.