题目内容
14.已知命题p:y=sin(x-$\frac{π}{2}}$)在(0,π)上是减函数;命题q:“a=$\sqrt{3}$”是“直线x=$\frac{π}{6}$为曲线f(x)=sinx+acosx的一条对称轴”的充要条件.则下列命题为真命题的是( )| A. | p∧q | B. | ¬p∧¬q | C. | ¬p∧q | D. | p∧¬q |
分析 分别判断出p,q的真假,从而判断出复合命题的真假.
解答 解:∵0<x<π,∴-$\frac{π}{2}$<x-$\frac{π}{2}$<$\frac{π}{2}$,
∴y=sin(x-$\frac{π}{2}}$)在(0,π)上是增函数,
命题p是假命题;
若a=$\sqrt{3}$,则f(x)=sinx+$\sqrt{3}$cosx=2($\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx)=2sin(x+$\frac{π}{3}$),
对称轴x+$\frac{π}{3}$=kπ+$\frac{π}{2}$,∴x=kπ+$\frac{π}{6}$,是充分条件,
若直线x=$\frac{π}{6}$为曲线f(x)=sinx+acosx的一条对称轴,
则f($\frac{π}{6}$-x)=f($\frac{π}{6}$+x) 当x=$\frac{π}{6}$即f(0)=f($\frac{π}{3}$)
∴f(0)=a=f($\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$+$\frac{a}{2}$,解得a=$\sqrt{3}$,
故命题q是真命题;
则命题¬p∧q是真命题,
故选:C.
点评 本题考查了三角函数问题,考查复合命题的真假,是一道基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
4.已知函数f(x)在R上满足f(-x)+f(x)=0,且x>0时,f(x)=$\frac{1}{2}$(|x+sinα|+|x+2sinα|)+$\frac{3}{2}$sinα(-$\frac{π}{2}$≤α≤$\frac{3π}{2}$)对任意的x∈R,都有f(x-3$\sqrt{3}$)≤f(x)恒成立,则实数α的取值范围为( )
| A. | [0,π] | B. | [-$\frac{π}{3}$,$\frac{2π}{3}$] | C. | [-$\frac{π}{6}$,$\frac{7π}{6}$] | D. | [-$\frac{π}{3}$,$\frac{4π}{3}$] |
2.用“秦九韶算法”计算多项式f(x)=x4+x-1,当x=2014时的值的过程中,需要做的加法运算和乘法运算次数分别是( )
| A. | 2,4 | B. | 4,4 | C. | 2,0 | D. | 4,2 |
19. 如图,直线在平面α外,直线m1,m2,n均在平面α内,若m1∥m2,且m1,m2均与n相交,下列能证明l⊥α的是( )
如图,直线在平面α外,直线m1,m2,n均在平面α内,若m1∥m2,且m1,m2均与n相交,下列能证明l⊥α的是( )
 如图,直线在平面α外,直线m1,m2,n均在平面α内,若m1∥m2,且m1,m2均与n相交,下列能证明l⊥α的是( )
如图,直线在平面α外,直线m1,m2,n均在平面α内,若m1∥m2,且m1,m2均与n相交,下列能证明l⊥α的是( )| A. | l⊥m1且l⊥m2 | B. | l⊥m1且l⊥n | C. | l⊥m1 | D. | l⊥n |
4.已知双曲线C的左右焦点分别为F1、F2,且F2恰为抛物线y2=8x的焦点.设A为双曲线C与该抛物线的一个交点,若△AF1F2是以AF1的底边的等腰三角形,则双曲线C的离心率为( )
| A. | 1+$\sqrt{3}$ | B. | 1+$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
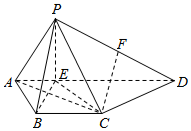 如图所示的几何体P-ABCD中,底面ABCD是梯形,且AD∥BC,点E是边AD上的一点,AE=BC=AB,AD=3BC,点F是PD的中点,PB⊥AC.
如图所示的几何体P-ABCD中,底面ABCD是梯形,且AD∥BC,点E是边AD上的一点,AE=BC=AB,AD=3BC,点F是PD的中点,PB⊥AC.