题目内容
已知数列{an}满足an+1=2an2-4an+3,且a1=3,an>1
(1)设bn=log2(an-1),证明数列{bn+1}为等比数列;
(2)设cn=(2n-1)bn,求数列{cn}的前n项和Sn.
(1)设bn=log2(an-1),证明数列{bn+1}为等比数列;
(2)设cn=(2n-1)bn,求数列{cn}的前n项和Sn.
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)由数列{an}满足an+1=2an2-4an+3,变形为an+1-1=2(an-1)2,两边取对数可得:log2(an+1-1)=2log2(an-1)+1,可得bn+1=2bn+1,变形为
bn+1+1=2(bn+1),即可证明.
(2)由(1)可得:bn=2n.cn=(2n-1)bn=(2n-1)•2n.再利用“错位相减法”、等比数列的前n项和公式即可得出.
bn+1+1=2(bn+1),即可证明.
(2)由(1)可得:bn=2n.cn=(2n-1)bn=(2n-1)•2n.再利用“错位相减法”、等比数列的前n项和公式即可得出.
解答:
(1)证明:由数列{an}满足an+1=2an2-4an+3,
变形为an+1-1=2(an-1)2,
∵a1=3,an>1,
∴两边取对数可得:log2(an+1-1)=2log2(an-1)+1,
∵bn=log2(an-1),
∴bn+1=2bn+1,
bn+1+1=2(bn+1),
又b1=log2(a1-1)=log2(3-1)=1.
∴数列{bn+1}为等比数列,首项为2,公比为2;
(2)解:由(1)可得:bn=2n.
∴cn=(2n-1)bn=(2n-1)•2n.
∴数列{cn}的前n项和Sn=2+3•22+5•23+…+(2n-1)•2n,
2Sn=22+3×23+…+(2n-3)•2n+(2n-1)•2n+1,
∴-Sn=2+2×22+2×23+…+2×2n-(2n-1)×2n+1=
-2-(2n-1)×2n+1=(3-2n)×2n+1-6,
∴Sn=(2n-3)×2n+1+6.
变形为an+1-1=2(an-1)2,
∵a1=3,an>1,
∴两边取对数可得:log2(an+1-1)=2log2(an-1)+1,
∵bn=log2(an-1),
∴bn+1=2bn+1,
bn+1+1=2(bn+1),
又b1=log2(a1-1)=log2(3-1)=1.
∴数列{bn+1}为等比数列,首项为2,公比为2;
(2)解:由(1)可得:bn=2n.
∴cn=(2n-1)bn=(2n-1)•2n.
∴数列{cn}的前n项和Sn=2+3•22+5•23+…+(2n-1)•2n,
2Sn=22+3×23+…+(2n-3)•2n+(2n-1)•2n+1,
∴-Sn=2+2×22+2×23+…+2×2n-(2n-1)×2n+1=
| 4(2n-1) |
| 2-1 |
∴Sn=(2n-3)×2n+1+6.
点评:本题考查了对数的运算性质、“错位相减法”、等比数列的通项公式及其前n项和公式,考查了变形能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知随机变量ξ服从正态分布N(1,σ2),若P(ξ>2)=0.15,则P(0≤ξ≤1)=( )
| A、0.85 | B、0.70 |
| C、0.35 | D、0.15 |
把函数y=sinx(x∈R)的图象上所有点向左平行移动
个单位长度,再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象所表示的函数是( )
| π |
| 3 |
A、y=sin(
| ||||
B、y=sin(
| ||||
C、y=sin(2x-
| ||||
D、y=sin(2x+
|
如图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次为A1,A2,…,A16,图2是茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )
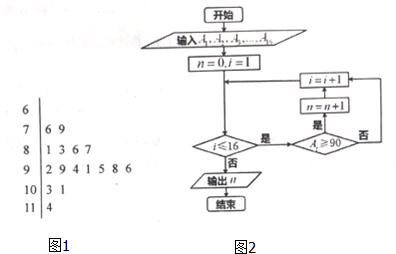

| A、6 | B、10 | C、91 | D、92 |
若函数y=f(2x+1)的定义域为[-1,2],则g(x)=f(x)+f(-x)的定义域是( )
| A、[-1,1] |
| B、[-5,5] |
| C、[-1,5] |
| D、[-5,1] |
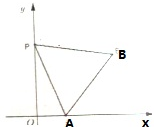 如图在平面内放置的边长为1的正三角形PAB沿x轴滚动,设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为
如图在平面内放置的边长为1的正三角形PAB沿x轴滚动,设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为