题目内容
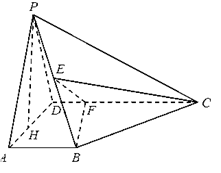
如图所示,在四棱锥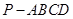 中,
中,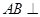 平面
平面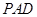 ,
,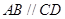 ,
,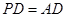 ,
,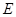 是
是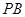 的中点,
的中点,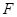 是
是 上的点且
上的点且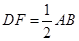 ,
,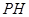 为△
为△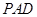 中
中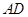 边上的高.
边上的高.
(1)证明: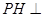 平面
平面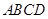 ;
;
(2)若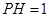 ,
,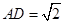 ,
,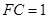 ,求三棱锥
,求三棱锥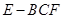 的体积;
的体积;
(3)证明: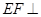 平面
平面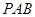 .
.
(1)见解析; (2)体积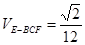 (3)见解析
(3)见解析
解析试题分析:(1)利用线面垂直的判断定理证明线面垂直,条件齐全.(2)利用棱锥的体积公式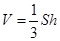 求体积.(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.
求体积.(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.(4)在求三棱柱体积时,选择适当的底作为底面,这样体积容易计算.
试题解析:(1)证明:因为 平面
平面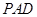 ,
,
所以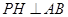 。
。
因为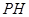 为△
为△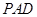 中
中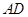 边上的高,
边上的高,
所以 。
。
因为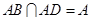 ,
,
所以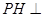 平面
平面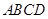 。 4分
。 4分
(2)连结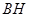 ,取
,取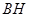 中点
中点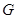 ,连结
,连结 。
。
因为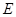 是
是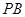 的中点,
的中点,
所以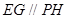 。
。
因为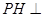 平面
平面 ,
,
所以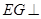 平面
平面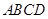 。
。
则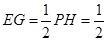 ,
,
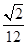 。 8分
。 8分
(3)证明:取 中点
中点 ,连结
,连结 ,
,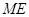 。
。
因为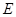 是
是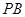 的中点, 所以
的中点, 所以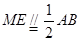 。
。
因为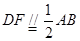 , 所以
, 所以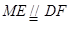 ,
,
所以四边形 是平行四边形,
是平行四边形,
所以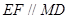 。
。
因为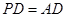 , 所以
, 所以 。
。
因为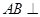 平面
平面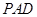 ,
,
所以 。
。
因为 , 所以
, 所以 平面
平面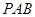 ,
,
所以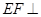 平面
平面 。 13分
。 13分
考点:(1)空间中线面垂直和平行的判定(2)几何体的体积.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
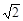 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.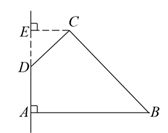
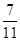
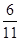
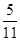
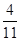
 及其三视图如图所示,过棱
及其三视图如图所示,过棱 的中点
的中点 作平行于
作平行于 ,
, 的平面分
的平面分 于点
于点 .
.
 是矩形;
是矩形; 的正弦值.
的正弦值.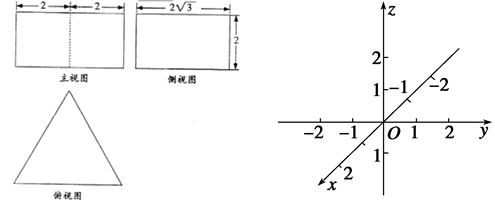
 平面
平面 ,且四边形
,且四边形 为矩形,四边形
为矩形,四边形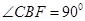 ,
,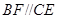 ,
,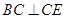 ,
,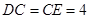 ,
,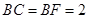 .
.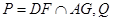 是直线
是直线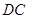 上的动点,判断并证明直线
上的动点,判断并证明直线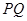 与直线
与直线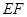 的位置关系.
的位置关系.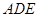 所成角的余弦值.
所成角的余弦值.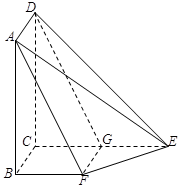
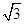 的正三棱锥
的正三棱锥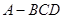 中,
中,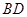 长为
长为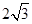 ,
,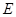 为棱
为棱 的中点,求
的中点,求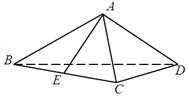
 与
与 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示); ), 则按图中尺寸,做成的工作台用去的合板的
), 则按图中尺寸,做成的工作台用去的合板的 。(制作过程合板损耗和合板厚度忽略不计)
。(制作过程合板损耗和合板厚度忽略不计)