Question

设f(x)是(－∞，＋∞)上的奇函数，f(x＋2)＝－f(x)，当0≤x≤1时，f(x)＝x.

(1)求f(π)的值；

(2)当－4≤x≤4时，求f(x)的图象与x轴所围图形的面积．

Answer 1

解析：(1)由f(x＋2)＝－f(x)，得                       

f(x＋4)＝f[(x＋2)＋2]＝－f(x＋2)＝f(x)，

所以f(x)是以4为周期的函数，从而得

f(π)＝f(－1×4＋π)＝f(π－4)＝－f(4－π)＝－(4－π)＝π－4.

(2)由f(x)是奇函数与f(x＋2)＝－f(x)，得f[(x－1)＋2]＝－f(x－1)＝f[－(x－1)]，

即f(1＋x)＝f(1－x)．

故知函数y＝f(x)的图象关于直线x＝1对称．

又0≤x≤1时，f(x)＝x，且f(x)的图象关于原点成中心对称，则f(x)的图象如图所示．

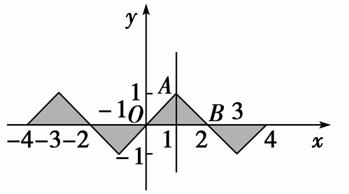
当－4≤x≤4时，f(x)的图象与x轴围成的图形面积为S，

则S＝4S_△OAB＝4×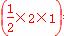＝4.