题目内容
17.在△ABC中,若$sin\frac{A}{2}=cos\frac{A+B}{2}$,则△ABC一定是( )| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
分析 由$\frac{A+B}{2}=\frac{π-C}{2}$,得sin$\frac{A}{2}$=sin$\frac{C}{2}$,⇒$\frac{A}{2}=\frac{C}{2}$,
解答 解:∵$sin\frac{A}{2}=cos\frac{A+B}{2}$=cos$\frac{π-C}{2}$=sin$\frac{C}{2}$,⇒$\frac{A}{2}=\frac{C}{2}$,则△ABC是等腰三角形,
故选:A.
点评 本题考查了三角形中三角和为π,及三角恒等变形,属于基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
8.圆(x+2)2+y2=5的圆心为( )
| A. | (2,0) | B. | (0,2) | C. | (-2,0) | D. | (0,-2) |
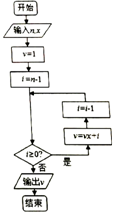 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )