题目内容
13.已知sinβ+cosβ=$\frac{\sqrt{5}}{5}$,且π<β<2π.(1)求sinβcosβ、sinβ-cosβ的值;
(2)求sinβ、cosβ、tanβ的值.
分析 (1)先把已知等式两边平方,求得2sinβcosβ即sin2β的值,同时可判断出β的范围,最后利用配方法求得sinβ-cosβ.
(2)利用已知条件以及(1)的结果,直接求解即可.
解答 解:(1)∵sinβ+cosβ=$\frac{\sqrt{5}}{5}$,
∴sin2β+cos2β+2sinβcosβ=$\frac{1}{5}$,
∴2sinβcosβ=-$\frac{4}{5}$<0,sinβ<0,cosβ>0,
∴$\frac{3π}{2}$<β<2π
∴sinβ-cosβ<0,
sinβ-cosβ=-$\sqrt{1-2sinβcosβ}$=-$\frac{3\sqrt{5}}{5}$,
(2)sinβ+cosβ=$\frac{\sqrt{5}}{5}$,sinβ-cosβ=-$\frac{3\sqrt{5}}{5}$,
可得sinβ=-$\frac{\sqrt{5}}{5}$,cosβ=$\frac{2\sqrt{5}}{5}$,
tanβ=-2.
点评 本题主要考查了同角三角函数基本关系的应用,二倍角公式的应用.解题过程中巧妙的利用sin2β+cos2β=1,利用配方法来解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
,
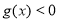 的解集;
的解集; ,均有
,均有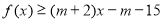 成立,求实数m的取值范围.
成立,求实数m的取值范围.