题目内容
设m，n都是不等于1的正数，并且logm3＞logn3，试比较m，n的大小．
考点：对数的运算性质
专题：函数的性质及应用
分析：对数图象的性质：在x=1的右侧底大图底，由此能求出结果．
解答：
解：m，n都是不等于1的正数，且logm3＞logn3，
①当0＜m＜1，0＜n＜1时，
利用对数图象的性质：在x=1的右侧底大图低，
得到1＞n＞m＞0．
②当m＞1，n＞1时，
利用对数图象的性质：在x=1的右侧底大图低，
得到n＞m＞1．
综上：n＞m．
①当0＜m＜1，0＜n＜1时，
利用对数图象的性质：在x=1的右侧底大图低，
得到1＞n＞m＞0．
②当m＞1，n＞1时，
利用对数图象的性质：在x=1的右侧底大图低，
得到n＞m＞1．
综上：n＞m．
点评：本题考查两个实数值大小的比较，是基础题，解题时要认真审题，注意对数性质的合理运用．
练习册系列答案
相关题目
对于推理：若a＞b，则a2＞b2，因为2＞-2，则22＞（-2）2，即4＞4，下列说法正确的是（ ）
| A、大前提错误 |
| B、小前提错误 |
| C、推理正确 |
| D、不是演绎推理 |
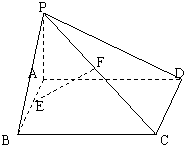如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB，PC的中点．
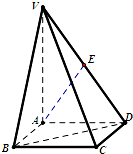如图，在四棱锥V-ABCD中，VA⊥底面ABCD，底面ABCD是边长为2的正方形．