题目内容
设a,b,c为ΔABC的三边,求证:方程x2+2ax+b2=0与x2+2cx-b2=0有公共根的充要条件是∠A=90°.
解析:充分性:∵∠A=90°,?
∴a2=b2+c2,于是方程x2+2ax+b2=0
可化为x2+2ax+a2-c2=0,?
∴x1=-(a+c),x2=c-a.?
同理,另一方程x2+2cx-b2=0可化为x2+2cx+c2-a2=0,?
可求得其两根为x3=-(a+c),x4=a-c,?
故两方程有公共根x1=x3=-(a+c),?
必要性:设α为两方程的公共根,?
则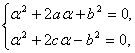 两式相加,
两式相加,
解得α=-(a+c),
∴(a+c)2-2a(a+c)+b2=0,?
∴b2+c2=a2,
∴∠A=90°.
综上,两方程有公共根的充要条件是∠A=90°.

练习册系列答案
相关题目
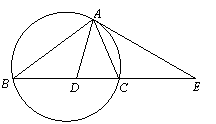 ∠BAC的平分线与BC交于点D.
∠BAC的平分线与BC交于点D.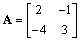 ,
,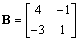 ,求满足
,求满足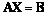 的二阶矩阵
的二阶矩阵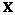 .
.