题目内容
设a,b,c为任意三角形三边长,I=a+b+c,S=ab+bc+ca,试证:I2<4S.
证明略
解析:
证明 由I2=(a+b+c)2
=a2+b2+c2+2(ab+bc+ca)
=a2+b2+c2+2S,
∵a,b,c为任意三角形三边长,
∴a<b+c,b<c+a,c<a+b,
∴a2<a(b+c),b2<b(c+a),c2<c(a+b)
即(a2-ab-ac)+(b2-bc-ba)+(c2-ca-cb)<0
∴a2+b2+c2-2(ab+bc+ca)<0
∴a2+b2+c2<2S
∴a2+b2+c2+2S<4S.
∴I2<4S.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 已知正三棱柱ABC-A′B′C′的正(主)视图和侧(左)视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,射线OA旋转所成的角为x弧度(x可以取到任意一个实数),对应的俯视图的面积为S(x),则函数S(x)的最大值为
已知正三棱柱ABC-A′B′C′的正(主)视图和侧(左)视图如图所示.设△ABC,△A′B′C′的中心分别是O,O′,现将此三棱柱绕直线OO′旋转,射线OA旋转所成的角为x弧度(x可以取到任意一个实数),对应的俯视图的面积为S(x),则函数S(x)的最大值为 已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O、O′,现将此三棱柱绕直线OO′旋转(包括逆时针方向和顺时针方向),射线OA旋转所成的角为x弧度(x可以取到任意一个实数),对应的俯视图的面积记为S(x),则函数S(x)的最大值和最小正周期分别是( )
已知正三棱柱ABC-A′B′C′的正视图和侧视图如图所示.设△ABC,△A′B′C′的中心分别是O、O′,现将此三棱柱绕直线OO′旋转(包括逆时针方向和顺时针方向),射线OA旋转所成的角为x弧度(x可以取到任意一个实数),对应的俯视图的面积记为S(x),则函数S(x)的最大值和最小正周期分别是( ) ,当
,当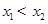 时,都有
时,都有 ,则称函数
,则称函数 在D上为非减函数 . 设函数f (x)在[0,1]上为非减函数,且满足以下三个条件:
在D上为非减函数 . 设函数f (x)在[0,1]上为非减函数,且满足以下三个条件: ;②
;②  ;③
;③ ,则
,则 等( )
等( ) B.
B.
 C.
1 D.
C.
1 D.

 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 在D上为非减函数. 设函数f (x)在[0,1]上为非减函数,且满足以下三个条件:1
在D上为非减函数. 设函数f (x)在[0,1]上为非减函数,且满足以下三个条件:1 ; 2
; 2 ; 3
; 3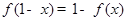 .
. 等于( )
等于( )  B.
B.
 C.
1
D.
C.
1
D. 