题目内容
设△ABC的内角A、B、C所对的边分别为a、b、c,且cosB=
,b=2.
(1)当A=
时,求a的值;
(2)当△ABC的面积为3时,求a+c的值.
| 4 |
| 5 |
(1)当A=
| π |
| 6 |
(2)当△ABC的面积为3时,求a+c的值.
(1)∵cosB=
,∴sinB=
.…(2分)
由正弦定理得
=
,可得
=
.…(4分)
∴a=
.…(6分)
(2)∵△ABC的面积S=
acsinB,sinB=
,
∴
ac=3,ac=10.…(8分)
由余弦定理b2=a2+c2-2accosB,…(9分)
得4=a2+c2-
ac=a2+c2-16,即a2+c2=20.…(10分)
∴(a+c)2-2ac=20,(a+c)2=40,…(11分)
∴a+c=2
.…(12分)
| 4 |
| 5 |
| 3 |
| 5 |
由正弦定理得
| a |
| sinA |
| b |
| sinB |
| a | ||
sin
|
| 10 |
| 3 |
∴a=
| 5 |
| 3 |
(2)∵△ABC的面积S=
| 1 |
| 2 |
| 3 |
| 5 |
∴
| 3 |
| 10 |
由余弦定理b2=a2+c2-2accosB,…(9分)
得4=a2+c2-
| 8 |
| 5 |
∴(a+c)2-2ac=20,(a+c)2=40,…(11分)
∴a+c=2
| 10 |

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
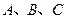 为
为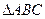 的三个内角,且其对边分别为
的三个内角,且其对边分别为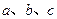 ,且
,且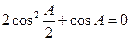 .(1)求角
.(1)求角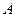 的值;
的值; (2)若
(2)若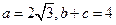 ,求
,求 ,
, ,
, .
.

 的值.
的值.