题目内容

在△ABC中，角A，B，C所对的边长分别为a，b，c，C=2A，a+c=10，cosA=
3
4
．
（1）求
c
a
的值；
（2）求b的值．
（1）∵C=2A，cosA=
3
4
，
∴由正弦定理得
c
a
=
sinC
sinA
=
sin2A
sinA
=
2sinAcosA
sinA
=2cosA=
3
2
；
（2）由
c
a
=
3
2
a+c=10
，
解得：
a=4
c=6
，
由余弦定理得a2=b2+c2-2bccosA，
∴16=b2+36-9b，整理得：b2-9b+20=0，
解得：b=4或b=5，
当b=4时，由C=2A，a=4，可知：B=45°，这与cosA=
3
4
矛盾，应舍去；
则b=5．
练习册系列答案
相关题目
（本小题满分14分）
先解答（1），再通过结构类比解答（2）：
（1）请用tanx表示，并写出函数的最小正周期；
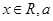（2）设为非零常数，且，试问是周期函数吗？证明你的结论.
设△ABC的内角A、B、C所对的边分别为a、b、c，且cosB=
4
5
，b=2．
（1）当A=
π
6
时，求a的值；
（2）当△ABC的面积为3时，求a+c的值．
设△ABC的内角A，B，C所对的边分别为a，b，c且acosC-
1
2
c=b．
（1）求角A的大小；
（2）若a=1，求△ABC的周长的取值范围．
（p1wu•北京）在△ABC中，a=u，b=p
6
，∠B=p∠A．
（Ⅰ）求cosA的值；
（Ⅱ）求c的值．
在△ABC中，内角A，B，C的对边分别为a，b，c，a=
2
，b=
3
，B=60°，则A=______．
在△ABC中，角A，B，C的对边分别为a，b，c，若a2+b2=4a+2b-5，且a2=b2+c2-bc，则sinB的值为______．
在△ABC中，已知a=4
3
，b=4，∠A=60°，则角B的度数为（　　）
A．30°或150°B．30°C．60°D．150°
已知△ABC的三个内角分别为A，B，C．
（1）若bcosA-acosB=0，且a=2，∠C=
π
4
，求c的值；
（2）若
a
=(cosA，sinB)，
b
=(cosB，sinA)，
a
•
b
=1，试判断三角形的形状？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网