题目内容
6.已知函数y=f(x)是周期为2的周期函数,且当时x∈[-1,1]时,f(x)=2|x|,则函数F(x)=f(x)-|lgx|的零点个数是( )| A. | 9 | B. | 10 | C. | 11 | D. | 18 |
分析 在坐标系中画出两个函数y1=|lgx|,y2=f(x)的图象,分析两个图象交点的个数,进而可得函数F(x)=f(x)-|lgx|的零点个数.
解答 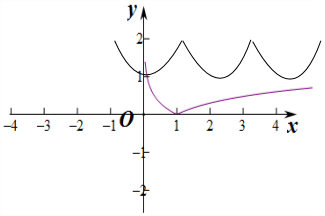 解:∵函数F(x)=f(x)-|lgx|的零点,
解:∵函数F(x)=f(x)-|lgx|的零点,
即为函数y1=|lgx|,y2=f(x)的图象的交点,
又∵函数y=f(x)是周期为2的周期函数,
且当x∈[-1,1]时,f(x)=2|x|,
在同一坐标系中画出两个函数y1=|lgx|,y2=f(x)的图象,如图所示:
由图可知:两个函数y1=|lgx|,y2=f(x)的图象共有9个交点,
故函数F(x)=f(x)-|lgx|有9个零点,
故选:A
点评 本题考查了函数零点、对应方程的根和函数图象之间的关系,通过转化和作图求出函数零点的个数.

练习册系列答案
相关题目
11.函数f(x)=x3-3x2在区间[-2,4]上的最大值为( )
| A. | -4 | B. | 0 | C. | 16 | D. | 20 |
12.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$,则目标函数z=x+2y+4的最小值为( )
| A. | 29 | B. | 25 | C. | 11 | D. | 9 |
9.已知条件p:|x+1|>2,条件q:x>a,且¬p是¬q的充分不必要条件,则a的取值范围是( )
| A. | a≤-3 | B. | a≤1 | C. | a≥-1 | D. | a≥1 |
11.已知命题P:至少存在一个实数x0∈[2,4],使不等式x2-ax+2>0成立.若P为真,则参数 a 的取值范围为( )
| A. | (-∞,3) | B. | $(-∞,2\sqrt{2})$ | C. | (-∞,$\frac{11}{3}$) | D. | (-∞,$\frac{9}{2}$) |
18.将函数$y=sin(\frac{1}{2}x-\frac{π}{6})$的图象上的所有的点横坐标缩短为原来的$\frac{1}{2}$(纵坐标不变),再将所得的图象向右平移$\frac{π}{3}$个单位,则所得的函数图象对应的解析式为( )
| A. | $y=cos(\frac{1}{4}x-\frac{π}{4})$ | B. | y=-sinx | C. | y=-cosx | D. | $y=sin(x+\frac{π}{6})$ |
15.有一算法流程图如图所示,该算法解决的是( )
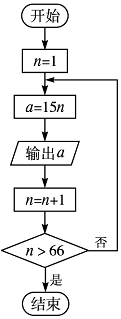

| A. | 输出不大于990且能被15整除的所有正整数 | |
| B. | 输出不大于66且能被15整除的所有正整数 | |
| C. | 输出67 | |
| D. | 输出能被15整除且大于66的正整数 |